Summatory functions

[Bodigrim]

Common difficulty of number theory is that arithmetic functions misbehave: their plots oscillate up and down in chaotic fashion. For instance, here is a plot of divisor function from wiki:

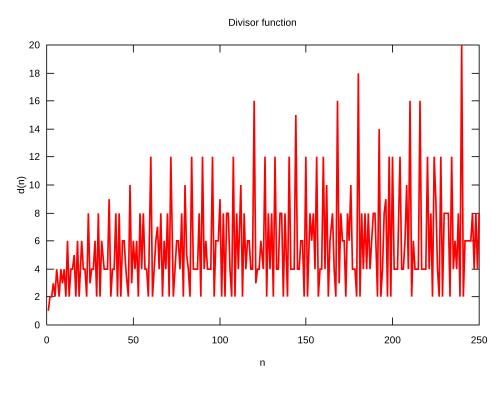
The pivot idea of analytic number theory is that instead of studying this jumble, we can study the summatory function, which is simply a sum (or an integral) of original function:

summatory :: (Int -> Int) -> Int -> Int 
summatory f n = sum $ map f [1..n]

Summatory functions behave well and a wide range of fruitful methods can be applied. E. g., divisor summatory function.

The interesting thing is that in many cases summatory function can be computed in sublinear time, faster than O(n). For example, let tau denote the divisor function. Then summatory tau n is equal to

2 * sum (map (\m -> x `quot` m) [1..sqrtx]) - sqrtx ^ 2

where sqrtx = integerSquareRoot x. This computation can be completed in O(x^{1/2}) time. There is a systematic way to derive such formulas, which I have explored in my old paper with a long title.

The proposal is to implement some of these algorithms, to provide users with a DSL to describe functions (in terms of Dirichlet convolution?) and to derive effective summatory formulas from DSL automatically.

Upd.: I think it is worse to create a separate type for multiplicative functions, accompanied by conversion multiplicative :: MultiplicativeFunction -> ArithmeticFunction, because there is so much more to do with multiplicative functions, which is undefined for general arithmetic ones. It would be nice to implement inverses of multiplicative functions as well, following the approach in Computing the inverses....

Implementation plan

• Function to evaluate arithmetic functions over intervals in quasilinear time (done in Bulk evaluation of arithmetic functions #77)
• Implement fast (O(x^2/3) time) summation of the Mobius function as per paper (done in Moebius and Mertens functions #90)
• Implement fast (O(x^1/3) time) summation of the divisor function as per paper. Help wanted
• Grab Faulhaber polynomials from Some Useful Polynomials and Other Series #70.
• Provide DSL to combine functions by Dirichlet convolution, deriving optimal summatory functions automatically as per paper.
• Review implementation of Math.NumberTheory.MoebiusInversion.totientSum.
• Compute inverses of multiplicative functions as per paper (done in Implement inverseTotient #142).

[CarlEdman]

Very interesting. I'll dig into that paper later. Until then I can offer one piece of Haskell code related to the sublinear computation of certain summatory functions over the primes. Its name is primeLucy (in honor of the infamous "Lucy Hedgehog" who first posted the algorithm which this code generalises).

It takes three parameters: A size parameter n::Integer, a function f:: Integer -> Integer, and its summatory function over the integers sf:: Integer -> Integer. It returns, in time of the order O(n^0.7) if I recall correctly, a summatory function g :: Integer -> Integer over the primes only. The summatory function is just a table lookup and hence instant, but is restricted to the parameters [1..sqrt n] and [n/sqrt(n), n/(sqrt(n)-1) .. n].

So, for example, (primeLucy (\x -> x*x*x) (\x -> div (((x+2)*x+1)*x*x) 4) n) n calculates the sum of the cubes of all primes up n. On my machine, it runs in 1.1s for n=10^10, 6.1s for n=10^11, and 31.6s for n=10^12. By comparison, even for n=10^8, the naive algorithm takes 8.6s on the same machine.

Here is the code for primeLucy. It isn't pretty, but it is fast and it could be made a great deal faster by restricting to functions with Int, rather than Integer, values and sums.

primeLucy f sf n = g
  where
    r = fromIntegral $ integerSquareRoot n :: Int
    ni = fromIntegral n :: Int
    loop from to c = let go i = ControlMonad.when (to<=i) (c i >> go (i-1)) in go from

    kf = ArrayST.runSTArray $ do
      k <- ArrayST.newListArray (-r,r) $ force $
        [sf (div n (toInteger i)) - sf 1|i<-[r,r-1..1]] ++
        [0] ++
        [sf (toInteger i) - sf 1|i<-[1..r]]
      ControlMonad.forM_ (takeWhile (<=r) $ map fromIntegral primes) $ \p -> do
        l <- ArrayST.readArray k (p-1)
        let q = force $ f (toInteger p)

        let adjust = \i j -> do { v <- ArrayBase.unsafeRead k (i+r); w <- ArrayBase.unsafeRead k (j+r); ArrayBase.unsafeWrite k (i+r) $!! v+q*(l-w) }

        loop (-1)         (-div r p)              $ \i -> adjust i (i*p)
        loop (-div r p-1) (-min r (div ni (p*p))) $ \i -> adjust i (div (-ni) (i*p))
        loop r            (p*p)                   $ \i -> adjust i (div i p)

      return k

    g :: Integer -> Integer
    g m
      | m >= 1 && m <= integerSquareRoot n                       = kf Array.! (fromIntegral m)
      | m >= integerSquareRoot n && m <= n && div n (div n m)==m = kf Array.! (fromIntegral (negate (div n m)))
      | otherwise = error $ "Function not precalculated for value " ++ show m

[Bodigrim]

Awesome, I was not aware of this algorithm.

I've found the original post of Lucy_Hedgehog (https://projecteuler.net/thread=10;page=5#111677). He mentions that "It is also possible to improve the complexity of the algorithm to O(n^2/3), but the code would be more complex". Do you know how?

[CarlEdman]

I am told the algorithm referred to there is described in the paper Tomás Oliveira e Silva, Computing pi(x): the combinatorial method, Revista do DETUA, but this paper is still on my reading list.

[Bodigrim]

I've just realised that there is Math.NumberTheory.Primes.Counting.Impl.primeCount, which boasts to count pi(x) (number of primes up to a given limit) in roughly O(n^0.7) time. The discussion above suggests that it can be generalised to compute a sum of values of an arbitrary function on primes, not just f p = 1, with the same time complexity. Sounds like a plan :)

[CarlEdman]

Hope you can use the code I posted above! It is more general that primeCount so it may be somewhat slower (though with the same asymptotics), but it's highly optimized, it gives you the value of the sum at a whole bunch of other useful points for free, and I have found it very useful, . Plenty of non-trivial Euler problems for which you just need to plug in a few simple functions into the algorithm to get the solution.

[ishandutta2007]

@Bodigrim

What @Lucy_Hedgehog wrote was generalised Legendre
I tried to code the Generalised Meissel Lehmer here.
More advanced algos for prime counting (in order of time complexity) are:

1798 : Legendre => $O(n^{3/4})$

1870 : Meissel => $O(n/log^{3}n)$

1959 : Lehmer => $O(n/log^{4}n)$ — popularly known as Miessel-Lehmer

1985 : Lagarias, Miller and Odlyzko => $O(n^{2/3})$ — popularly known as LMO

1996 : M. Deleglise, J. Rivat => $O(n^{2/3}/log^2n)$

2001 : Xavier Gourdon => $O(n^{2/3} / log^2n)$ (constant factor for both time and memory improved) — default algo for Kimwalisch's package

2015 : Douglas Staple => $O(n^{2/3} / log^2n)$ (constant factor for memory improved)

Each of them can be generalised to find sum of primes or even sum of squares of primes. @kimwalisch have generalised most of them in repo primesum