Skip to content

Data Placement Strategies

Jump to bottom
H. Joe Lee edited this page Jan 18, 2022 · 7 revisions

HERMES Setting

Every Hermes system instance includes one or more Hermes nodes.

A destination is a buffering resource that can be identified by a pair of node + target "coordinates."

Each target $t_k$ has characteristics such as the following:

  • A capacity $Cap[t_k]$
  • A remaining capacity $Rem[t_k]$
  • A speed (or throughput) $Speed[...,t_k]$
    • This is the mean of the throughputs of all ranks associated with the destination's node.
    • Fix this! Speed is really a function of the origin.

Note: At any point in time, there's a degree of uncertainty to some of the destination characteristics. For example, the remaining capacity of a destination is typically obtained from a global metadata (MD) structure that is updated asynchronously. Only the Hermes node buffer pool managers have the precise value(s) for the pool under their management.

The Data Placement Problem

Given N storage targets, a data placement policy P, a cost function F, and a BLOB.

A data placement consists of a BLOB partitioning and an assignment of those parts to storage targets that satisfies the constraints of the data placement policy and that minimizes the cost function.

  • Epoch - interval within which we update targets (status).
    • Static (e.g., time interval or number of operations)
    • Dynamic, i.e., computed by the delta of status

[optional] Placement window - interval within which we make data placement decisions.

  • Timer expired or I/O operation count reached, which ever comes first.
  • Static (e.g., time interval or number of operations)
  • Dynamic, i.e., number of put operations

Epoch and placement window could be aligned (static mode)

The data placement is done within Data Placement Engine (DPE) component in HERMES.

The Data Placement Loop

A placement schema $PS(b)$ of a BLOB $b (>0)$ is a decompostion $b = s_1+\cdots+s_k,\; s_i\in\mathbb{N}\setminus\{0\}$ together with a target mapping $(s_1,\ldots,s_k)\mapsto(t_1(s_1),\ldots,t_k(s_k))$.

A sequence of buffer IDs $(ID_1,\ldots,ID_A)$ conforms to a target assignment $(s, t)$, iff $s = \sum_{i=1}^A Size(ID_i)$ and $\forall i\;Target(ID_i) = t$.

An allocation of a placement schema is a sequence of buffer IDs which is the concatenation of conforming target assignments.

  1. Given: a vector of BLOBs $(b_1, b_2,\ldots, b_B)$
  2. The DPE creates placement schemas $PS(b_i),\;1\leq i\leq B$
  3. The placement schemas are presented to the buffer manager, which, for each placement schema, returns an allocation of that schema (or an error), and updates the underlying metadata structures.
  4. I/O clients transfer data from the BLOBs to the buffers.

Problem to Solve in DPE

Input:

  • Vector of BLOBs $(b_1, b_2,\ldots, b_B)$.
  • Vector of targets $(t_1, t_2,\ldots, t_D)$.
  • Vector of target remaining capacities $Rem[t_k], \;1\leq k\leq D$.
  • Vector of target speed $Speed[t_k], \;1\leq k\leq D$.

OutputL

  • Placement schema $(s_1,\ldots,s_k)\mapsto(t_1(s_1),\ldots,t_k(s_k))$, where $b (>0)$ is a decompostion $b = s_1+\cdots+s_k,\; s_i\in\mathbb{N}\setminus\{0\}$

Data Placement Solution

  1. Pick a DP solver to obtain a placement schema
    • Linear programming
      • Constraints
      • Objective function
    • Round-robin
      • Granularity
    • Random
      • Distribution(s)
  2. Use the buffer pool's "coin selector" to convert into buffer IDs
  3. Handle two types of potential errors
    • DP solver failure: This can happen because of outdated target status, i.e. insufficient capacity, constraint infeasibility, etc.
      • Solution to insufficient capacity: epoch, decision windows, swap space.
      • Solution to constraint infeasibility: buffer reorganization, target filtering.
    • Coin selection failure: This can happen because of outdated state view information, e.g., outdated remaining capacities.
      • Solution: epoch, decision windows, swap space.

Error Handling

In both cases, the list of targets is inappropriate and needs to be updated or changed.

The list of "relevant destinations" for a rank is assembled by the Hermes node topology generator. It gets triggered when DP fails. The initial topology consists of "node-local" destinations (Plan A) plus a backup list of neighbors (Plan B) to consult when a rank gets in trouble. If both plans fail, the topology generator invokes the application-level "rebalancer" to redraw neighborhood boundaries. (Plan C) In the past, we used to call these components node- and application-level DPEs, but they aren't directly involved in DP decisions, and we need maybe a clearer terminology.

Data Placement Solution Implementation

LP solver

  • Pick Google OR-Tools as a linear optimization tool to obtain a placement schema
    • Minimize client I/O time.

Round-robin solver

  • Pick the next target if the remaining capacity is greater or equal to the BLOB size, otherwise check the one after the next target until a target with enough capacity is found.

Random solver

  • Randomly pick a target from all targets which have the capacity greater or equal to the BLOB size.

Experimental Setup

Scaling the number of blobs, 10 GB total blob size

  • Small size blobs: random within the range of 4KB to 64KB
  • Medium size blobs: random within the range of 64KB to 1MB
  • Large size blobs: random within the range of 1MB to 4MB
  • Extra large size blobs: random with the range 4MB to 64MB
  • Huge size blobs: fixed 1GB

Scaling the blob size, 1000 and 8192 blobs in total

  • Fixed blob size of 4KB, 64KB, 1MB, 4MB, 64MB

Experimental Results

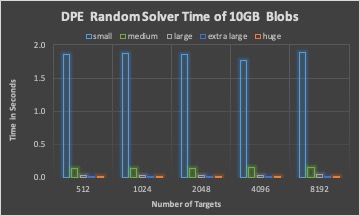
The DPE time of three different solvers with 10GB Blobs in total.

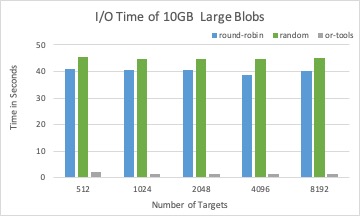
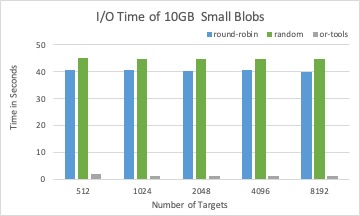
The associated I/O time of placement schema from three different solvers with 10GB Blobs in total.

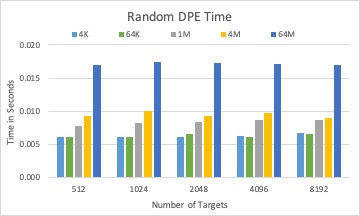
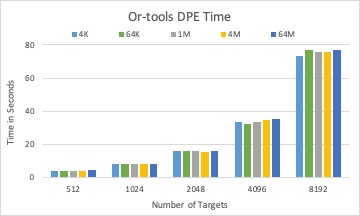
The DPE time of three different solvers with 1000 Blobs in total.

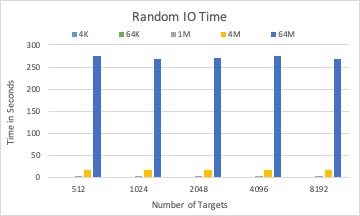
The associated I/O time by placement schema by three different solvers with 1000 Blobs in total.

Conclusions

For a fixed total size of many blobs, dpe time is increasing with the number of blobs for all solvers.

Round-robin and random solver can quickly calculate targets for a blob than LP solver, while not considering optimizing I/O time.

LP solver is efficient when the search space (number of targets) is not too large (for example less than 1024)

LP solver is a good candidate to place large size blobs, where the dpe time has less impact than the I/O time to the overall performance.

One of the possible policies is that size 64KB could be a boundary for blob aggregation. Blob size less than 64KB will be aggregated within a placement window and than placed together to mitigate dpe impact.

Another possible policy is to use round-robin or random for small blobs and LP solver for large blobs.

Clone this wiki locally