给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:
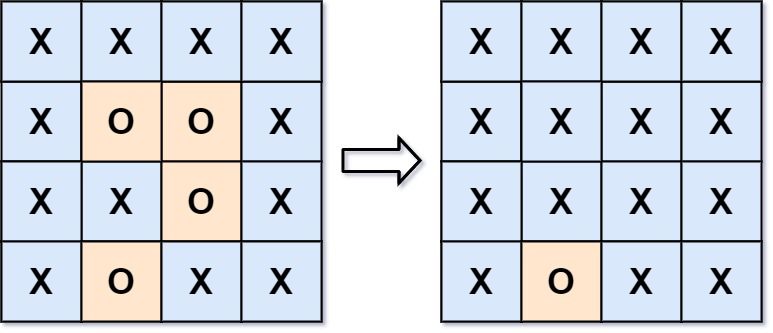
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] 解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的'O'都不会被填充为'X'。 任何不在边界上,或不与边界上的'O'相连的'O'最终都会被填充为'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]] 输出:[["X"]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]为'X'或'O'
dfs/bfs 均可
/**
Do not return anything, modify board in-place instead.
*/
function solve(board: string[][]): void {
let m = board.length, n = board[0].length;
if (m < 3 || n < 3) return;
let visited = Array.from({ length: m }, v => new Array(n).fill(false));
// 第一行,最后一行, 第一列, 最后一列
for (let i of [0, m-1]) {
for (let j = 0; j < n; ++j) {
if (board[i][j] == 'X') {
visited[i][j] = true;
} else {
dfs(board, i, j, visited, true);
}
}
}
for (let i = 0; i < m; ++i) {
for (let j of [0, n - 1]) {
if (board[i][j] == 'X') {
visited[i][j] = true;
} else {
dfs(board, i, j, visited, true);
}
}
}
for (let i = 1; i < m - 1; ++i) {
for (let j = 1; j < n - 1; ++j) {
!visited[i][j] && dfs(board, i, j, visited);
}
}
};
function dfs(board: string[][], i: number, j: number, visited: boolean[][], edge = false): void {
let m = board.length, n = board[0].length;
if (i < 0 || i > m - 1 || j < 0 || j > n - 1 || visited[i][j]) {
return;
}
visited[i][j] = true;
if (board[i][j] == 'X') {
return;
}
if (!edge) {
board[i][j] = 'X';
}
for (let [dx, dy] of [[0, 1], [0, -1], [1, 0], [-1, 0]]) {
let x = i + dx, y = j + dy;
dfs(board, x, y, visited, edge);
}
}