class-14.md

Implementation: Trees

• tutorial about Binary Trees, Binary Search Trees, and K-ary Trees.

• Terminology:

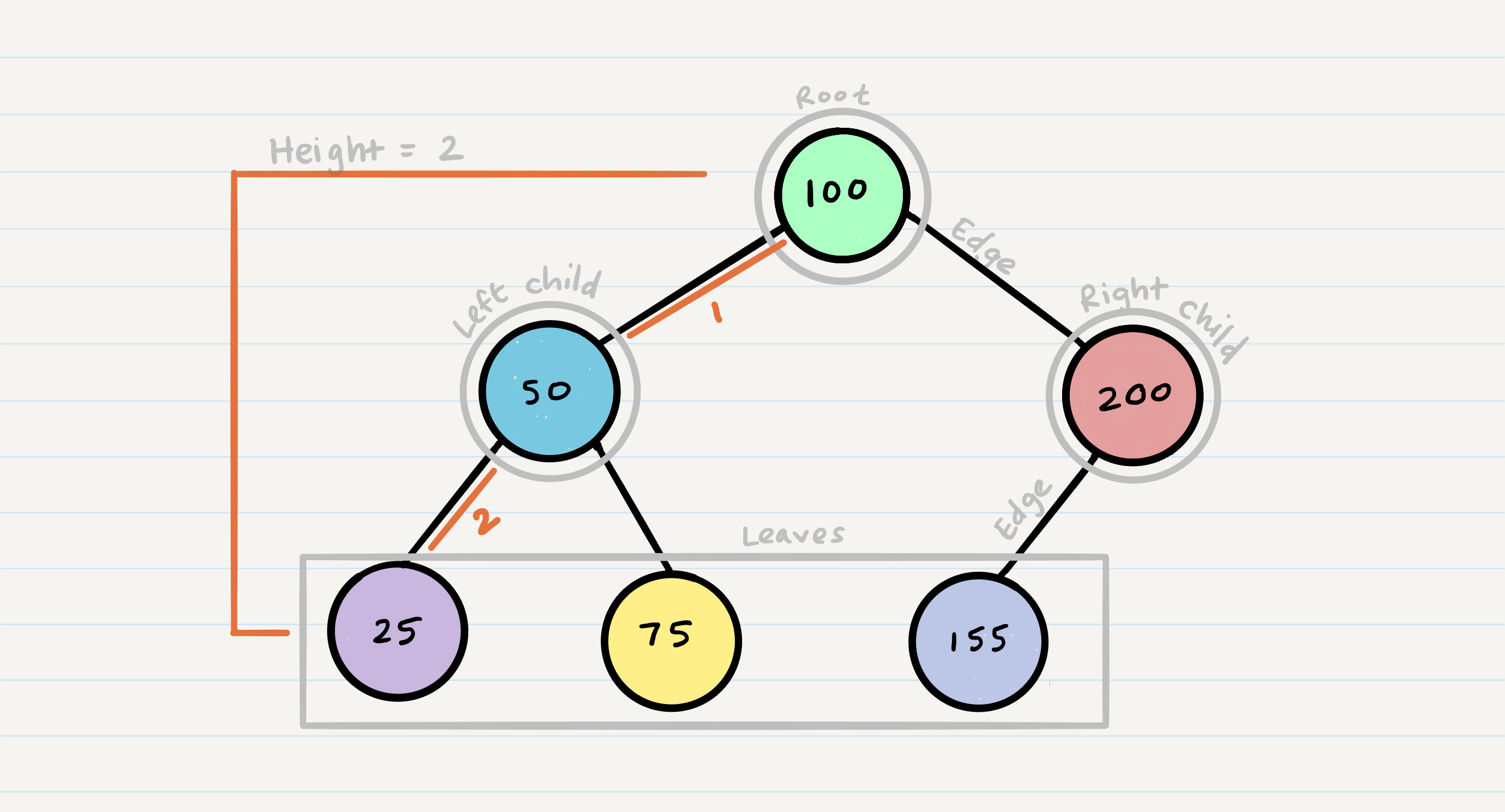
  • Tree Node: a node contain value, and two references: right and left.
  • Root: the first node in the tree.
  • left : a reference hold a node as value in the node.
  • right: a reference hold a node as value in the node.
  • edge : a connection between parent node and child node.
  • leaf node: a node has no children.
  • tree height: the total number of edges between root and the deepest leaf.
  • K - A : number specify the max number of children that node can have.

• Tree Example:

Traversing tree (iterate)

• There are two types of or ways of traversing tree.
  • Depth First.
  • breadth First.

1. Depth First:
   • Depth first visit tree nodes from root to the down end of tree node by node.
   • It uses Stack.
   • There are 3 methods to iterate using depth:
     • pre order depth.
     • in order depth.
     • post order depth.

Pre Order

• pre order where traversing start from root and accessing each element on the left first then do something to the left leaf.

• it uses recursion.

• Mechanism: 1. first method preOrder(root) called and passed root to it. 2. add the root value to stack. 3. check if it's left node not null then call method again. 4. if null check it's right node if it's not null call method again. 5. if both right and left are null it will pop() root from stack and check for higher level node than root. 6. if no higher node it will stop calling the preOrder(root). 7. it will apply this pattern on all nodes in the tree

• Pseudocode for each method:

  • Pre-Order:

public void preOrder(root):

   print = root.value

    if root.left not null 
            preOrder(root.left)
    if root.right not null
            preorder(root.right)

• In-Order:

public void preOrder(root):

    if root.left not null 
            preOrder(root.left)
    
    print = root.value

    if root.right not null
            preorder(root.right)

• Post-Order:

public void preOrder(root):

    if root.left not null 
            preOrder(root.left)
    if root.right not null
            preorder(root.right)
    
     print = root.value

1. Breadth First:

• visit tree nodes From top level to last level from left to right then enqueue values.

• so it first enqueue root, then next children level enqueue and so on.

• it uses queue.

• Pseudocode for Breadth

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while breadth.peek()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    if front.left is not NULL
      breadth.enqueue(front.left)

    if front.right is not NULL
      breadth.enqueue(front.right)

resource Code Fellows

Binary Tree Vs K-ary Trees

• implementation above was on binary tree.
• a binary tree can have up to 2 nodes left and right maximum.

k-ary Tree

• it's similar to binary tree, but the different is It can have k number of children.
• a tree can have k number of children is called k-ary.
• K Refer to the number of children the k-ary tree have.
• To implement Breadth first, it works similar to binary search but instead I will apply algorithm on K children.

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while breadth.peek()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    for child in front.children
        breadth.enqueue(child)

resource Code Fellows.

Adding a node

• It does not matter where to add new node in tree.
• that's why I can use the breadth first.
• it will go down to the children and start adding from left to right.
• if I want to add the new node to a specific place, I have to get the parent first, then add the new value.

Big O

• for adding new node it will always be O(n) beause trees has no specific way of organizing for data.
• because breadth first, search from left to right visiting all nodes in the tree can be used to insert new element in the tree.

Binary Search Trees (BST)

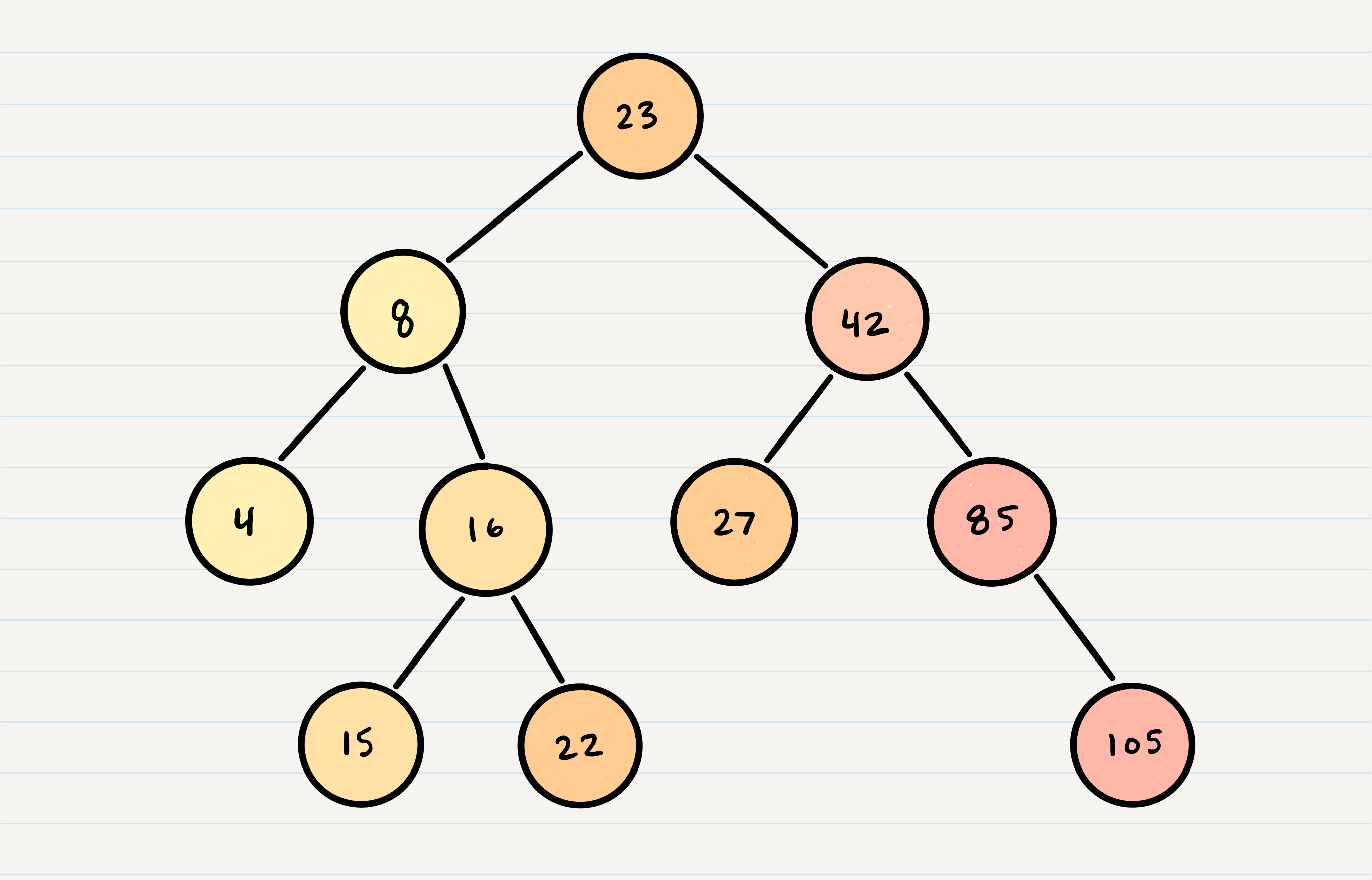
• binary search special type of tree.
• Nodes contain max up to 2 children.
• Perfect BST is where each non-leaf node contain only 2 childrn.
• Nodes on the left are always smaller than the root.
• Nodes on the right are always larger than the root.
• Notice in the image how it's ordered.

Big O

• tutorial say it's O(h) the height of the tree.
• worse case is where I will visit all nodes which is O(n).