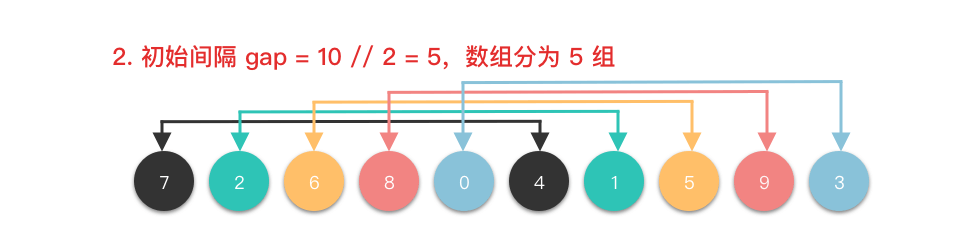
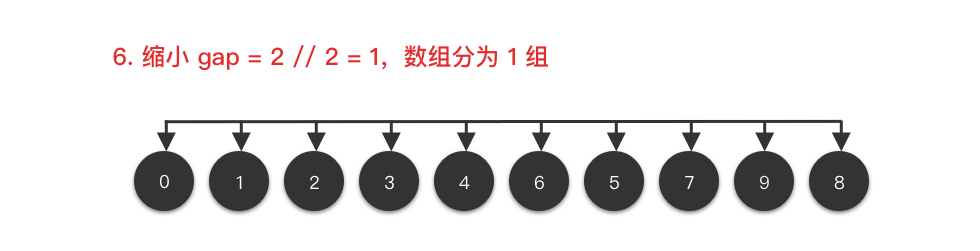
希尔排序(Shell Sort)基本思想:
将整个数组切按照一定的间隔取值划分为若干个子数组,每个子数组分别进行插入排序。然后逐渐缩小间隔进行下一轮划分子数组和对子数组进行插入排序。直至最后一轮排序间隔为
$1$ ,对整个数组进行插入排序。
假设数组的元素个数为
- 确定一个元素间隔数
$gap$ 。 - 将参加排序的数组按此间隔数从第
$1$ 个元素开始一次分成若干个子数组,即分别将所有位置相隔为$gap$ 的元素视为一个子数组。 - 在各个子数组中采用某种排序算法(例如插入排序算法)进行排序。
- 减少间隔数,并重新将整个数组按新的间隔数分成若干个子数组,再分别对各个子数组进行排序。
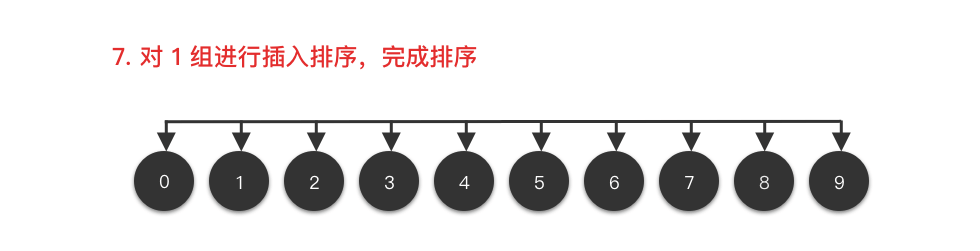
- 依次类推,直到间隔数
$gap$ 值为$1$ ,最后进行一次排序,排序结束。
我们以
::: tabs#shellSort
@tab <1>
@tab <2>
@tab <3>
@tab <4>
@tab <5>
@tab <6>
@tab <7>
:::
class Solution:
def shellSort(self, nums: [int]) -> [int]:
size = len(nums)
gap = size // 2
# 按照 gap 分组
while gap > 0:
# 对每组元素进行插入排序
for i in range(gap, size):
# temp 为每组中无序数组第 1 个元素
temp = nums[i]
j = i
# 从右至左遍历每组中的有序数组元素
while j >= gap and nums[j - gap] > temp:
# 将每组有序数组中插入位置右侧的元素依次在组中右移一位
nums[j] = nums[j - gap]
j -= gap
# 将该元素插入到适当位置
nums[j] = temp
# 缩小 gap 间隔
gap = gap // 2
return nums
def sortArray(self, nums: [int]) -> [int]:
return self.shellSort(nums)-
时间复杂度:介于
$O(n \times \log^2 n)$ 与$O(n^2)$ 之间。- 希尔排序方法的速度是一系列间隔数
$gap_i$ 的函数,而比较次数与$gap_i$ 之间的依赖关系比较复杂,不太容易给出完整的数学分析。 - 本文采用
$gap_i = \lfloor gap_{i-1}/2 \rfloor$ 的方法缩小间隔数,对于具有$n$ 个元素的数组,如果$gap_1 = \lfloor n/2 \rfloor$ ,则经过$p = \lfloor \log_2 n \rfloor$ 趟排序后就有$gap_p = 1$ ,因此,希尔排序方法的排序总躺数为$\lfloor \log_2 n \rfloor$ 。 - 从算法中也可以看到,外层
while gap > 0的循环次数为$\log n$ 数量级,内层插入排序算法循环次数为$n$ 数量级。当子数组分得越多时,子数组内的元素就越少,内层循环的次数也就越少;反之,当所分的子数组个数减少时,子数组内的元素也随之增多,但整个数组也逐步接近有序,而循环次数却不会随之增加。因此,希尔排序算法的时间复杂度在$O(n \times \log^2 n)$ 与$O(n^2)$ 之间。
- 希尔排序方法的速度是一系列间隔数
-
空间复杂度:$O(1)$。希尔排序中用到的插入排序算法为原地排序算法,只用到指针变量
$i$ 、$j$ 以及表示无序区间中第$1$ 个元素的变量、间隔数$gap$ 等常数项的变量。 -
排序稳定性:在一次插入排序是稳定的,不会改变相等元素的相对顺序,但是在不同的插入排序中,相等元素可能在各自的插入排序中移动。因此,希尔排序方法是一种 不稳定排序算法。