双指针(Two Pointers):指的是在遍历元素的过程中,不是使用单个指针进行访问,而是使用两个指针进行访问,从而达到相应的目的。如果两个指针方向相反,则称为「对撞指针」。如果两个指针方向相同,则称为「快慢指针」。如果两个指针分别属于不同的数组 / 链表,则称为「分离双指针」。
在数组的区间问题上,暴力算法的时间复杂度往往是
对撞指针:指的是两个指针
$left$ 、$right$ 分别指向序列第一个元素和最后一个元素,然后$left$ 指针不断递增,$right$ 不断递减,直到两个指针的值相撞(即$left == right$ ),或者满足其他要求的特殊条件为止。
- 使用两个指针
$left$ ,$right$。$left$ 指向序列第一个元素,即:$left = 0$,$right$ 指向序列最后一个元素,即:$right = len(nums) - 1$。 - 在循环体中将左右指针相向移动,当满足一定条件时,将左指针右移,$left += 1$。当满足另外一定条件时,将右指针左移,$right -= 1$。
- 直到两指针相撞(即
$left == right$ ),或者满足其他要求的特殊条件时,跳出循环体。
left, right = 0, len(nums) - 1
while left < right:
if 满足要求的特殊条件:
return 符合条件的值
elif 一定条件 1:
left += 1
elif 一定条件 2:
right -= 1
return 没找到 或 找到对应值对撞指针一般用来解决有序数组或者字符串问题:
- 查找有序数组中满足某些约束条件的一组元素问题:比如二分查找、数字之和等问题。
- 字符串反转问题:反转字符串、回文数、颠倒二进制等问题。
下面我们根据具体例子来讲解如何使用对撞指针来解决问题。
描述:给定一个下标从
要求:从数组中找出满足相加之和等于
说明:
-
$2 \le numbers.length \le 3 * 10^4$ 。 -
$-1000 \le numbers[i] \le 1000$ 。 -
$numbers$ 按非递减顺序排列。 -
$-1000 \le target \le 1000$ 。 - 仅存在一个有效答案。
示例:
- 示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。- 示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。这道题如果暴力遍历数组,从中找到相加之和等于
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
size = len(numbers)
for i in range(size):
for j in range(i + 1, size):
if numbers[i] + numbers[j] == target:
return [i + 1, j + 1]
return [-1, -1]结果不出意外的超时了。所以我们要想办法减少时间复杂度。
可以考虑使用对撞指针来减少时间复杂度。具体做法如下:
- 使用两个指针
$left$ ,$right$。$left$ 指向数组第一个值最小的元素位置,$right$ 指向数组值最大元素位置。 - 判断两个位置上的元素的和与目标值的关系。
- 如果元素和等于目标值,则返回两个元素位置。
- 如果元素和大于目标值,则让
$right$ 左移,继续检测。 - 如果元素和小于目标值,则让
$left$ 右移,继续检测。
- 直到
$left$ 和$right$ 移动到相同位置停止检测。 - 如果最终仍没找到,则返回
$[-1, -1]$ 。
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left = 0
right = len(numbers) - 1
while left < right:
total = numbers[left] + numbers[right]
if total == target:
return [left + 1, right + 1]
elif total < target:
left += 1
else:
right -= 1
return [-1, -1]- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。只用到了常数空间存放若干变量。
描述:给定一个字符串
要求:判断是否为回文串(只考虑字符串中的字母和数字字符,并且忽略字母的大小写)。
说明:
- 回文串:正着读和反着读都一样的字符串。
-
$1 \le s.length \le 2 * 10^5$ 。 -
$s$ 仅由可打印的 ASCII 字符组成。
示例:
输入: "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。
输入:"race a car"
输出:false
解释:"raceacar" 不是回文串。- 使用两个指针
$left$ ,$right$。$left$ 指向字符串开始位置,$right$ 指向字符串结束位置。 - 判断两个指针对应字符是否是字母或数字。 通过
$left$ 右移、$right$ 左移的方式过滤掉字母和数字以外的字符。 - 然后判断
$s[start]$ 是否和$s[end]$ 相等(注意大小写)。- 如果相等,则将
$left$ 右移、$right$ 左移,继续进行下一次过滤和判断。 - 如果不相等,则说明不是回文串,直接返回
$False$ 。
- 如果相等,则将
- 如果遇到
$left == right$ ,跳出循环,则说明该字符串是回文串,返回$True$ 。
class Solution:
def isPalindrome(self, s: str) -> bool:
left = 0
right = len(s) - 1
while left < right:
if not s[left].isalnum():
left += 1
continue
if not s[right].isalnum():
right -= 1
continue
if s[left].lower() == s[right].lower():
left += 1
right -= 1
else:
return False
return True- 时间复杂度:$O(len(s))$。
- 空间复杂度:$O(len(s))$。
描述:给定
要求:找出其中的两条线,使得它们与
说明:
-
$n == height.length$ 。 -
$2 \le n \le 10^5$ 。 -
$0 \le height[i] \le 10^4$ 。
示例:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。从示例中可以看出,如果确定好左右两端的直线,容纳的水量是由「左右两端直线中较低直线的高度 * 两端直线之间的距离」所决定的。所以我们应该使得「」,这样才能使盛水面积尽可能的大。
可以使用对撞指针求解。移动较低直线所在的指针位置,从而得到不同的高度和面积,最终获取其中最大的面积。具体做法如下:
- 使用两个指针
$left$ ,$right$。$left$ 指向数组开始位置,$right$ 指向数组结束位置。 - 计算
$left$ 和$right$ 所构成的面积值,同时维护更新最大面积值。 - 判断
$left$ 和$right$ 的高度值大小。- 如果
$left$ 指向的直线高度比较低,则将$left$ 指针右移。 - 如果
$right$ 指向的直线高度比较低,则将$right$ 指针左移。
- 如果
- 如果遇到
$left == right$ ,跳出循环,最后返回最大的面积。
class Solution:
def maxArea(self, height: List[int]) -> int:
left = 0
right = len(height) - 1
ans = 0
while left < right:
area = min(height[left], height[right]) * (right-left)
ans = max(ans, area)
if height[left] < height[right]:
left += 1
else:
right -= 1
return ans- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
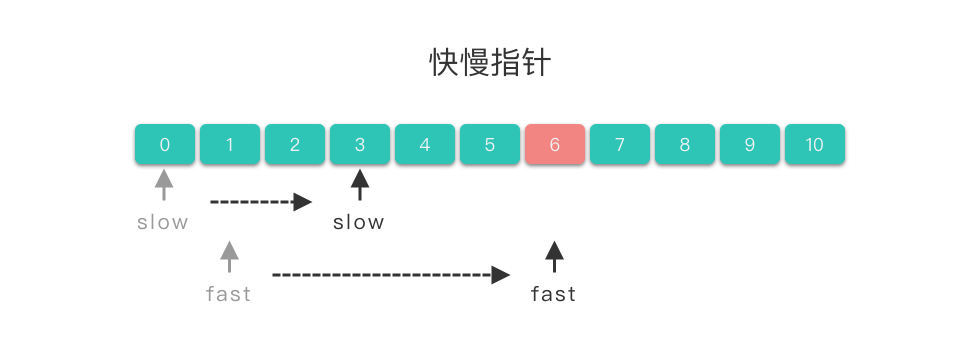
快慢指针:指的是两个指针从同一侧开始遍历序列,且移动的步长一个快一个慢。移动快的指针被称为 「快指针(fast)」,移动慢的指针被称为「慢指针(slow)」。两个指针以不同速度、不同策略移动,直到快指针移动到数组尾端,或者两指针相交,或者满足其他特殊条件时为止。
- 使用两个指针
$slow$ 、$fast$。$slow$ 一般指向序列第一个元素,即:$slow = 0$,$fast$ 一般指向序列第二个元素,即:$fast = 1$。 - 在循环体中将左右指针向右移动。当满足一定条件时,将慢指针右移,即
$slow += 1$ 。当满足另外一定条件时(也可能不需要满足条件),将快指针右移,即$fast += 1$ 。 - 到快指针移动到数组尾端(即
$fast == len(nums) - 1$ ),或者两指针相交,或者满足其他特殊条件时跳出循环体。
slow = 0
fast = 1
while 没有遍历完:
if 满足要求的特殊条件:
slow += 1
fast += 1
return 合适的值快慢指针一般用于处理数组中的移动、删除元素问题,或者链表中的判断是否有环、长度问题。关于链表相关的双指针做法我们到链表章节再详细讲解。
下面我们根据具体例子来讲解如何使用快慢指针来解决问题。
描述:给定一个有序数组
要求:删除数组
说明:
- 不能使用额外的数组空间,在原地修改数组,并在使用
$O(1)$ 额外空间的条件下完成。
示例:
- 示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。- 示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。因为数组是有序的,那么重复的元素一定会相邻。
删除重复元素,实际上就是将不重复的元素移到数组左侧。考虑使用双指针。具体算法如下:
- 定义两个快慢指针
$slow$ ,$fast$。其中$slow$ 指向去除重复元素后的数组的末尾位置。$fast$ 指向当前元素。 - 令
$slow$ 在后,$fast$ 在前。令$slow = 0$ ,$fast = 1$。 - 比较
$slow$ 位置上元素值和$fast$ 位置上元素值是否相等。- 如果不相等,则将
$slow$ 右移一位,将$fast$ 指向位置的元素复制到$slow$ 位置上。
- 如果不相等,则将
- 将
$fast$ 右移$1$ 位。 - 重复上述
$3 \sim 4$ 步,直到$fast$ 等于数组长度。 - 返回
$slow + 1$ 即为新数组长度。
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
if len(nums) <= 1:
return len(nums)
slow, fast = 0, 1
while (fast < len(nums)):
if nums[slow] != nums[fast]:
slow += 1
nums[slow] = nums[fast]
fast += 1
return slow + 1- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
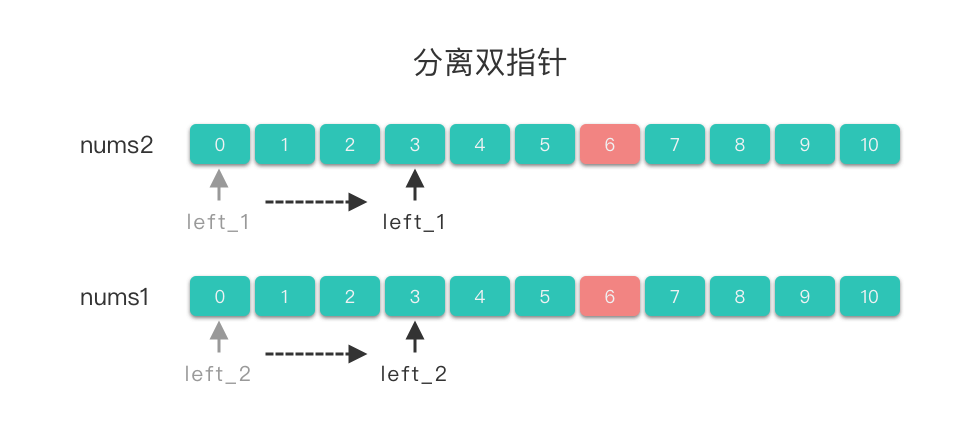
分离双指针:两个指针分别属于不同的数组,两个指针分别在两个数组中移动。
- 使用两个指针
$left\underline{}1$ 、$left\underline{}2$。$left\underline{}1$ 指向第一个数组的第一个元素,即:$left\underline{}1 = 0$,$left\underline{}2$ 指向第二个数组的第一个元素,即:$left\underline{}2 = 0$。 - 当满足一定条件时,两个指针同时右移,即
$left\underline{}1 += 1$ 、$left\underline{}2 += 1$。 - 当满足另外一定条件时,将
$left\underline{}1$ 指针右移,即$left\underline{}1 += 1$ 。 - 当满足其他一定条件时,将
$left\underline{}2$ 指针右移,即$left\underline{}2 += 1$ 。 - 当其中一个数组遍历完时或者满足其他特殊条件时跳出循环体。
left_1 = 0
left_2 = 0
while left_1 < len(nums1) and left_2 < len(nums2):
if 一定条件 1:
left_1 += 1
left_2 += 1
elif 一定条件 2:
left_1 += 1
elif 一定条件 3:
left_2 += 1分离双指针一般用于处理有序数组合并,求交集、并集问题。
下面我们根据具体例子来讲解如何使用分离双指针来解决问题。
描述:给定两个数组
要求:返回两个数组的交集。重复元素只计算一次。
说明:
-
$1 \le nums1.length, nums2.length \le 1000$ 。 -
$0 \le nums1[i], nums2[i] \le 1000$ 。
示例:
- 示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:- 示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的- 对数组
$nums1$ 、$nums2$ 先排序。 - 使用两个指针
$left\underline{}1$ 、$left\underline{}2$。$left\underline{}1$ 指向第一个数组的第一个元素,即:$left\underline{}1 = 0$,$left\underline{}2$ 指向第二个数组的第一个元素,即:$left\underline{}2 = 0$。 - 如果
$nums1[left\underline{}1] == nums2[left\underline{}2]$ ,则将其加入答案数组(注意去重),并将$left\underline{}1$ 和$left\underline{}2$ 右移。 - 如果
$nums1[left\underline{}1] < nums2[left\underline{}2]$ ,则将$left\underline{}1$ 右移。 - 如果
$nums1[left\underline{}1] > nums2[left\underline{}2]$ ,则将$left\underline{}2$ 右移。 - 最后返回答案数组。
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
nums1.sort()
nums2.sort()
left_1 = 0
left_2 = 0
res = []
while left_1 < len(nums1) and left_2 < len(nums2):
if nums1[left_1] == nums2[left_2]:
if nums1[left_1] not in res:
res.append(nums1[left_1])
left_1 += 1
left_2 += 1
elif nums1[left_1] < nums2[left_2]:
left_1 += 1
elif nums1[left_1] > nums2[left_2]:
left_2 += 1
return res- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
双指针分为「对撞指针」、「快慢指针」、「分离双指针」。
- 对撞指针:两个指针方向相反。适合解决查找有序数组中满足某些约束条件的一组元素问题、字符串反转问题。
- 快慢指针:两个指针方向相同。适合解决数组中的移动、删除元素问题,或者链表中的判断是否有环、长度问题。
- 分离双指针:两个指针分别属于不同的数组 / 链表。适合解决有序数组合并,求交集、并集问题。