Skip to content

Latest commit

 

History

History
257 lines (196 loc) · 8.72 KB

intro.md

File metadata and controls

257 lines (196 loc) · 8.72 KB
Raw

Learn the Basics

This chapter introduces the basic conception of rotated object detection and the framework of MMRotate, and provides links to detailed tutorials about MMRotate.

What is rotated object detection

Problem definition

Benefiting from the vigorous development of general object detection, most current rotated object detection models are based on classic general object detector. With the development of detection tasks, horizontal boxes have been unable to meet the needs of researchers in some subdivisions. We call it rotating object detection by redefining the object representation and increasing the number of regression degrees of freedom to achieve rotated rectangle, quadrilateral, and even arbitrary shape detection. Performing high-precision rotated object detection more efficiently has become a current research hotspot. The following areas are where rotated object detection has been applied or has great potential: face recognition, scene text, remote sensing, self-driving, medical, robotic grasping, etc.

What is rotated box

The most notable difference between rotated object detection and generic detection is the replacement of horizontal box annotations with rotated box annotations. They are defined as follows:

  • Horizontal box: A rectangle with the width along the x-axis and height along the y-axis. Usually, it can be represented by the coordinates of 2 diagonal vertices (x_i, y_i) (i = 1, 2), or it can be represented by the coordinates of the center point and the width and height, (x_center, y_center, width, height).
  • Rotated box: It is obtained by rotating the horizontal box around the center point by an angle, and the definition method of its rotated box is obtained by adding a radian parameter (x_center, y_center, width, height, theta), where theta = angle * pi / 180. The unit of theta is rad. When the rotation angle is a multiple of 90°, the rotated box degenerates into a horizontal box. The rotated box annotations exported by the annotation software are usually polygons, which need to be converted to the rotated box definition method before training.
In MMRotate, angle parameters are in radians.

Rotation direction

A rotated box can be obtained by rotating a horizontal box clockwise or counterclockwise around its center point. The rotation direction is closely related to the choice of the coordinate system. The image space adopts the right-handed coordinate system (y, x), where y is up->down and x is left->right. There are two opposite directions of rotation:

  • Clockwise（CW）

Schematic of CW

0-------------------> x (0 rad)
|  A-------------B
|  |             |
|  |     box     h
|  |   angle=0   |
|  D------w------C
v
y (pi/2 rad)

Rotation matrix of CW

\begin{pmatrix}
\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha
\end{pmatrix}

Rotation transformation of CW

P_A=
\begin{pmatrix} x_A \\ y_A\end{pmatrix}
=
\begin{pmatrix} x_{center} \\ y_{center}\end{pmatrix} +
\begin{pmatrix}\cos\alpha & -\sin\alpha \\
\sin\alpha & \cos\alpha\end{pmatrix}
\begin{pmatrix} -0.5w \\ -0.5h\end{pmatrix} \\
=
\begin{pmatrix} x_{center}-0.5w\cos\alpha+0.5h\sin\alpha
\\
y_{center}-0.5w\sin\alpha-0.5h\cos\alpha\end{pmatrix}
  • Counterclockwise（CCW）

Schematic of CCW

0-------------------> x (0 rad)
|  A-------------B
|  |             |
|  |     box     h
|  |   angle=0   |
|  D------w------C
v
y (-pi/2 rad)

Rotation matrix of CCW

\begin{pmatrix}
\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha
\end{pmatrix}

Rotation transformation of CCW

P_A=
\begin{pmatrix} x_A \\ y_A\end{pmatrix}
=
\begin{pmatrix} x_{center} \\ y_{center}\end{pmatrix} +
\begin{pmatrix}\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha\end{pmatrix}
\begin{pmatrix} -0.5w \\ -0.5h\end{pmatrix} \\
=
\begin{pmatrix} x_{center}-0.5w\cos\alpha-0.5h\sin\alpha
\\
y_{center}+0.5w\sin\alpha-0.5h\cos\alpha\end{pmatrix}

The operators that can set the rotation direction in MMCV are:

  • box_iou_rotated (Defaults to CW)
  • nms_rotated (Defaults to CW)
  • RoIAlignRotated (Defaults to CCW)
  • RiRoIAlignRotated (Defaults to CCW).
In MMRotate, the rotation direction of the rotated boxes is `CW`.

Definition of rotated box

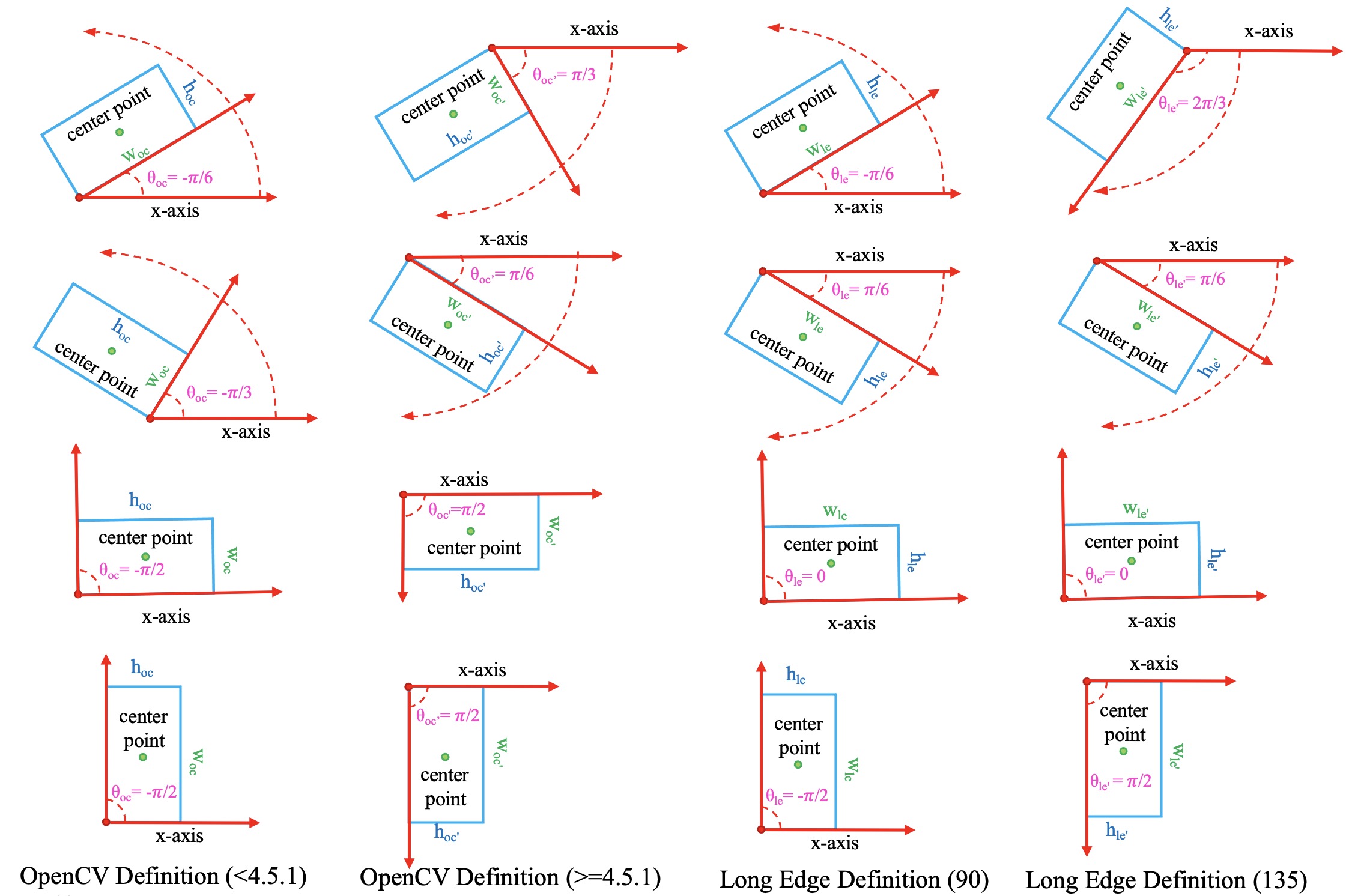
Due to the difference in the definition range of theta, the following three definitions of the rotated box gradually emerge in rotated object detection:

  • {math}D_{oc^{\prime}}: OpenCV Definition, angle∈(0, 90°], theta∈(0, pi / 2], The angle between the width of the rectangle and the positive semi-axis of x is a positive acute angle. This definition comes from the cv2.minAreaRect function in OpenCV, which returns an angle in the range (0, 90°].
  • {math}D_{le135}: Long Edge Definition (135°)，angle∈[-45°, 135°), theta∈[-pi / 4, 3 * pi / 4) and width > height.
  • {math}D_{le90}: Long Edge Definition (90°)，angle∈[-90°, 90°), theta∈[-pi / 2, pi / 2) and width > height.

The conversion relationship between the three definitions is not involved in MMRotate, so we will not introduce it much more. Refer to the below blog to dive deeper.

MMRotate supports the above three definitions of rotated box simultaneously,
which can be flexibly switched through the configuration file.

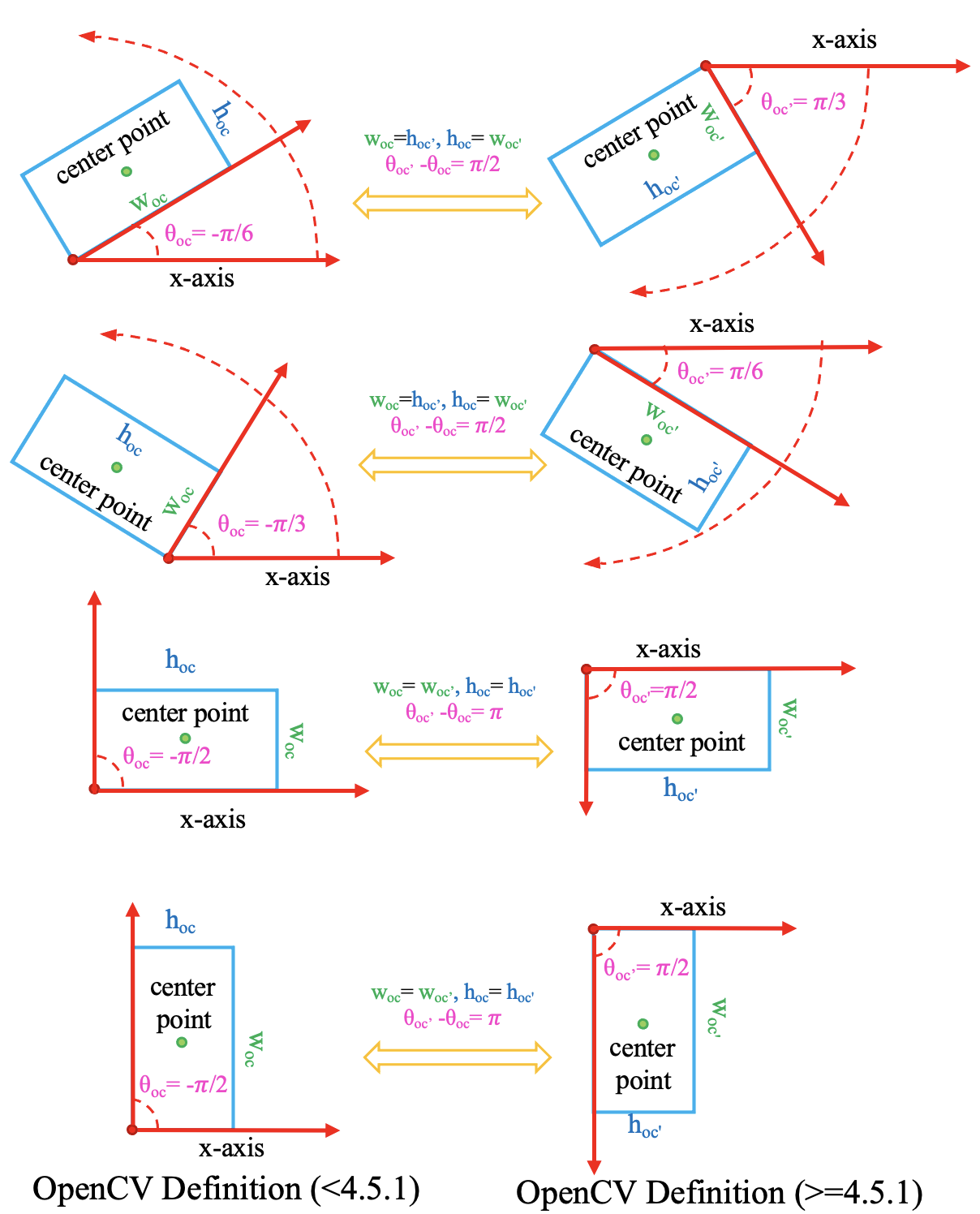
It should be noted that if the OpenCV version is less than 4.5.1, the angle range of cv2.minAreaRect is between [-90°, 0°). Reference In order to facilitate the distinction, the old version of the OpenCV definition is denoted as {math}D_{oc}.

  • {math}D_{oc^{\prime}} : OpenCV definition, opencv>=4.5.1, angle∈(0, 90°], theta∈(0, pi / 2].
  • {math}D_{oc} : Old OpenCV definition, opencv<4.5.1, angle∈[-90°, 0°), theta∈[-pi / 2, 0).

The conversion relationship between the two OpenCV definitions is as follows:

D_{oc^{\prime}}\left( w_{oc^{\prime}},h_{oc^{\prime}},\theta _{oc^{\prime}} \right) =\begin{cases}
	D_{oc}\left( h_{oc},w_{oc},\theta _{oc}+\pi /2 \right) , otherwise\\
	D_{oc}\left( w_{oc},h_{oc},\theta _{oc}+\pi \right) ,\theta _{oc}=-\pi /2\\
\end{cases}
\\
D_{oc}\left( w_{oc},h_{oc},\theta _{oc} \right) =\begin{cases}
	D_{oc^{\prime}}\left( h_{oc^{\prime}},w_{oc^{\prime}},\theta _{oc^{\prime}}-\pi /2 \right) , otherwise\\
	D_{oc^{\prime}}\left( w_{oc^{\prime}},h_{oc^{\prime}},\theta _{oc^{\prime}}-\pi \right) , \theta _{oc^{\prime}}=\pi /2\\
\end{cases}

Regardless of the OpenCV version you are using, MMRotate will convert the theta
of the OpenCV definition to (0, pi / 2].

Evaluation

The code for evaluating mAP involves the calculation of IoU. We can directly calculate the IoU of the rotated boxes or convert the rotated boxes to a polygons and then calculate the polygons IoU (DOTA online evaluation uses the calculation of polygons IoU).

What is MMRotate

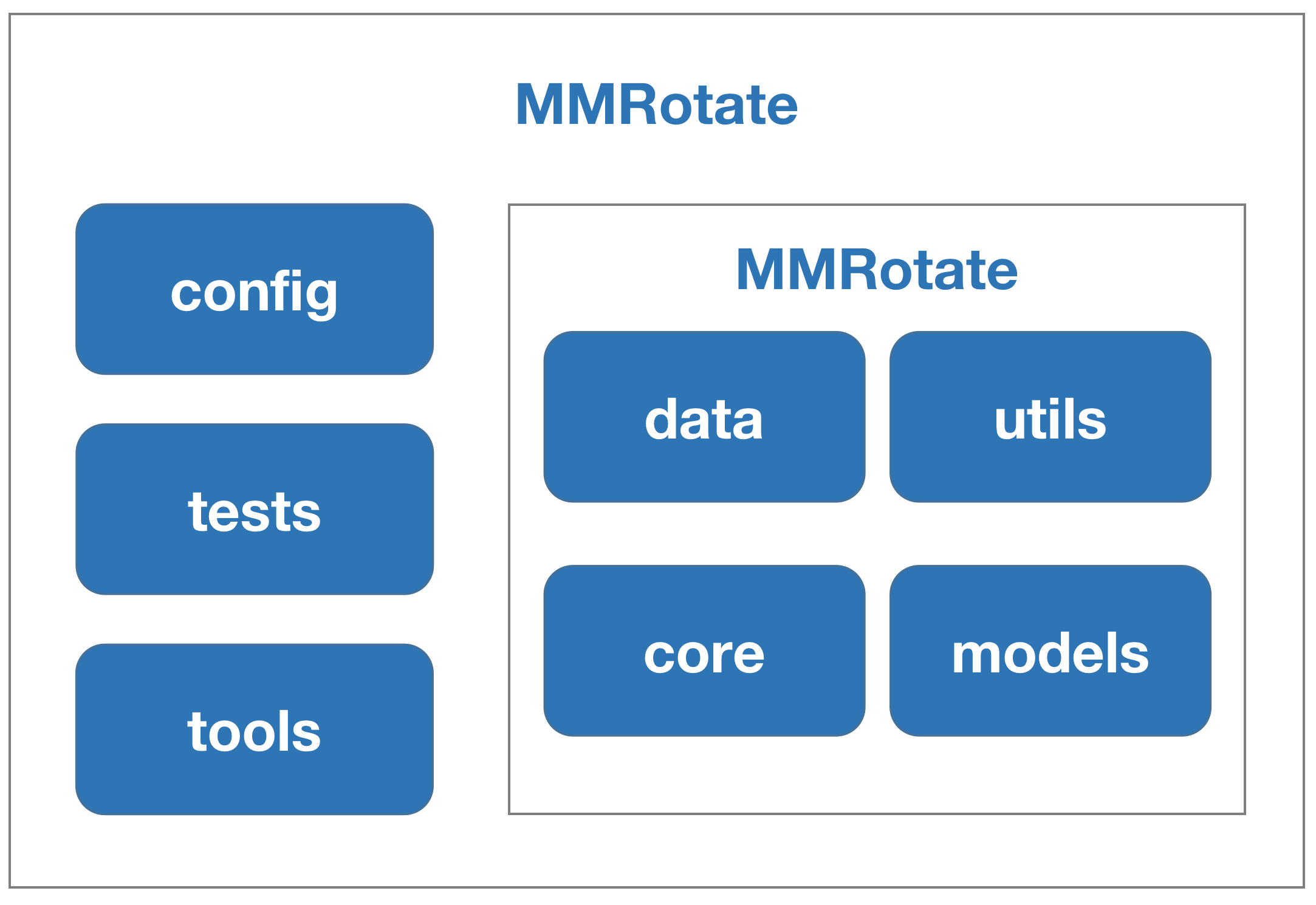
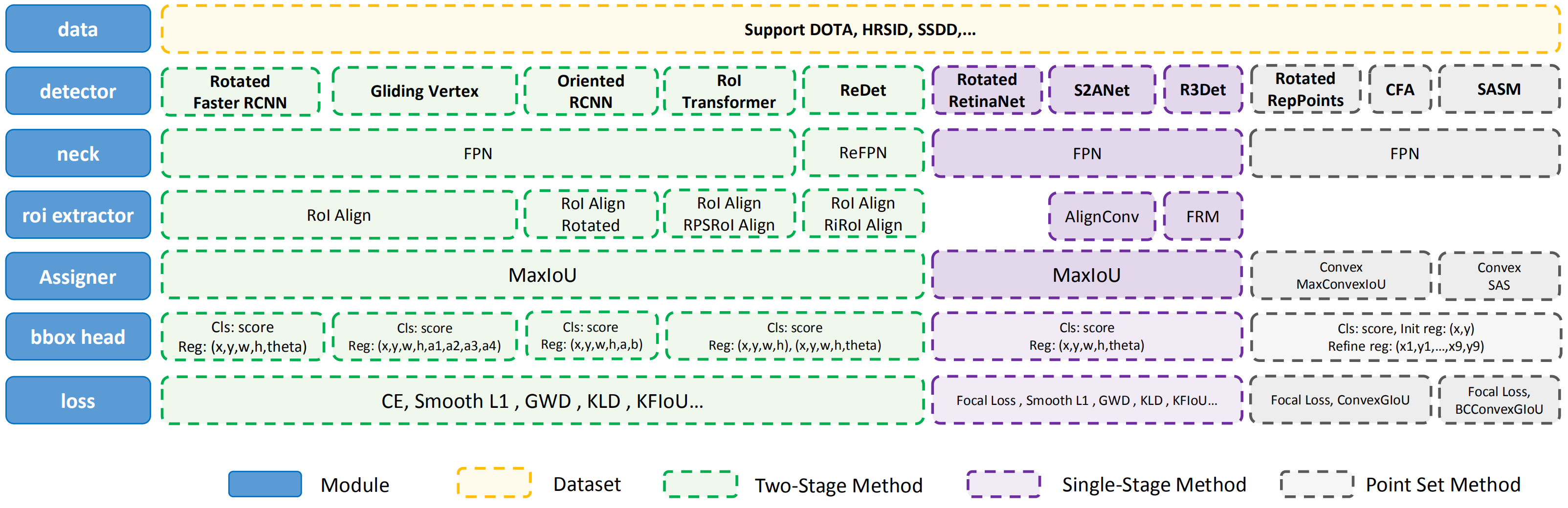
MMRotate is a toolbox that provides a framework for unified implementation and evaluation of rotated object detection, and below is its whole framework:

MMRotate consists of 4 main parts, datasets, models, core and apis.

  • datasets is for data loading and data augmentation. In this part, we support various datasets for rotated object detection algorithms, useful data augmentation transforms in pipelines for pre-processing image.

  • models contains models and loss functions.

  • core provides evaluation tools for model training and evaluation.

  • apis provides high-level APIs for models training, testing, and inference.

The module design of MMRotate is as follows:

The following points need to be noted due to different definitions of rotated box:

  • Loading annotations
  • Data augmentation
  • Assigning samples
  • Evaluation

How to Use this Guide

Here is a detailed step-by-step guide to learn more about MMRotate:

  1. For installation instructions, please see install.

  2. get_started is for the basic usage of MMRotate.

  3. Refer to the below tutorials to dive deeper: