README.md

Floating Point

Fractional Binary Numbers

A floating-point representation encodes rational number of the form $V = x * 2^y$. It's useful for performing computations involving very large numbers, numbers very close to 0, and more generally as an approximation to real arithmetic.

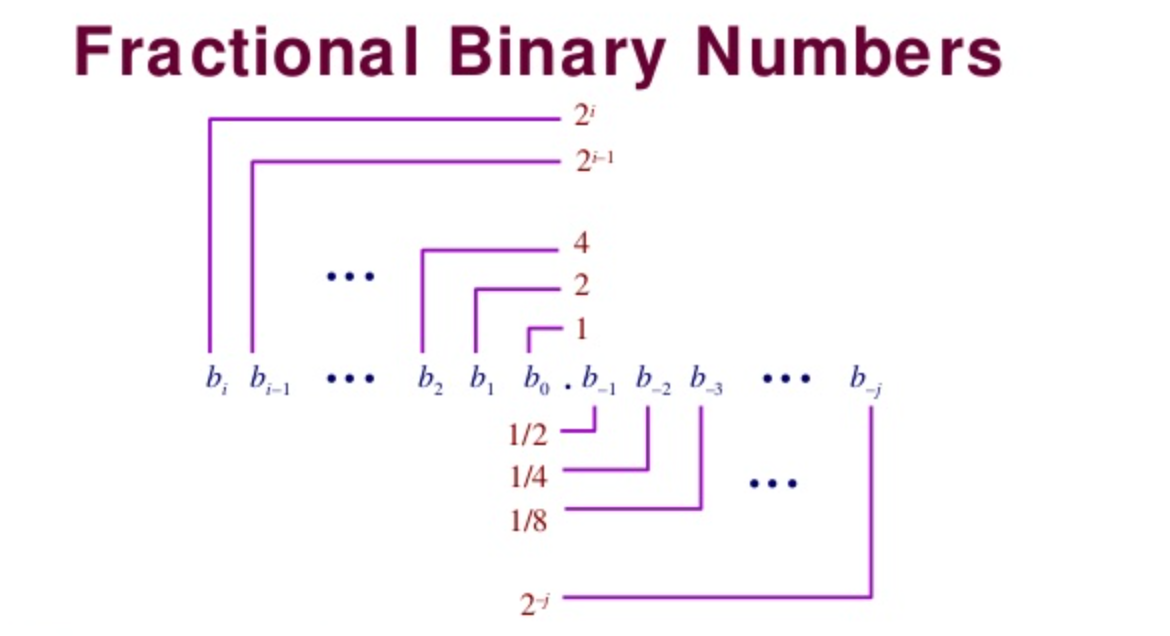
This notation represents a number b defined as $b = \sum_{k=-j}^i 2^k * b_k$.

Here are some practices:

• 2.45
• 2.46

IEEE Floating-Point Representation

The IEEE floating-point standard represents a number in a form $V = (-1)^s M 2^E$

• The sign s determines whether the number is negative(s = 1) or positive(s = 0).
• The exponent E weights the value by a power of 2.
• The significand M is a fractional binary number.

Case 1: Normalized Values

If exp is neither all zeros nor all ones, in this case, this exp field is interpreted as representing a baised form. That is, the exp value is $E = e - Bias$, where Bias is a bias value.

And $M = 1 + f$, where $ 0 \le f < 1$, having binary representation $0.f_{n-1}...f_1f_0$.

Case 2: Denormalized Values

When the exp field is all zeros, the represented number is in denormalized form. In this case, the exp value is $E = 1 - Bias$ rather than $-Bias$,and the significand value is $M = f$, that is, the value of the fraction field without an implied leading 1.

Denormalized numbers server two purposes. First, they provide a way to represent numeric value 0, since with a normalized number wwe must always have $M \ge 1$, and hence we can't represent 0. Second, represent numbers that are very close to 0.0.

Case 3: Special value

A final category of values occurs when the exp field is all ones.

• When the fraction filed is all zeros, the resulting values represent infinity, either positive inf when s = 0, and negative inf when s = 1. It can represent results that overflow, as when we multiply two very large numbers, or when we divide by zero.

• When the fraction field is nonzero, the resulting value is called Nan, short for "not a number". As when computing $\sqrt{-1}$.

• 2.47

• 2.48

• 2.49

Rounding

Floating-point arithmetic can only approximate real arithmetic, since the representation has limited range and precision. Thus, for a value $x$, we generally want a systematic method of finding the closest matching value $x'$ that can be represented in the desired floating-point format. This is the task of rounding operation.

Here are four rounding modes:

Mode	1.4	1.6	1.5	2.5	-1.5
Round-to-even	1	2	2	3	-2
Round-toward-zero	1	1	1	2	-1
Round-down	1	1	1	2	-2
Round-up	2	2	2	3	-1

Some practices:

• 2.50
• 2.51
• 2.52

Floating-Point Operations

Because of rounding, floating-point operations:

• lack of associativity: a + b + c may not equal a + c + b.
• if a >= b, x + a >= x + b.
• lack of distributivity.

And casting values between int, float, double:

• From int to float, the number can't overflow, but it may be rounded.
• From int or float to double,the exact numeric value can be preserved.
• From double to float, the value can overflow or rounded.
• From float or double to int, the value will be rounded toward zero. And the value may overflow.

Some practices:

• 2.53
• 2.54