Skip to content

Latest commit

 

History

History
93 lines (71 loc) · 2.53 KB

README.md

File metadata and controls

93 lines (71 loc) · 2.53 KB

Optala: Numerical Optimizations in Scala

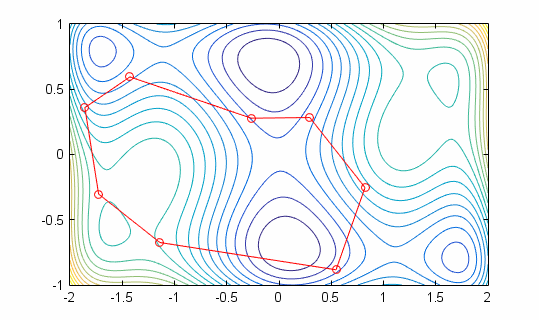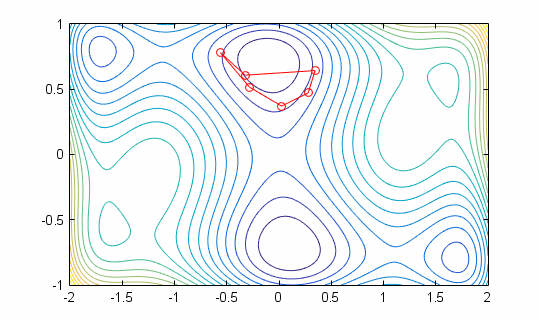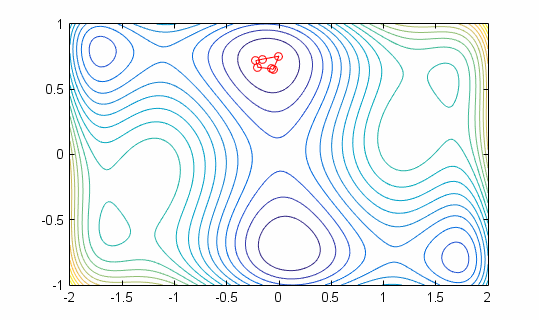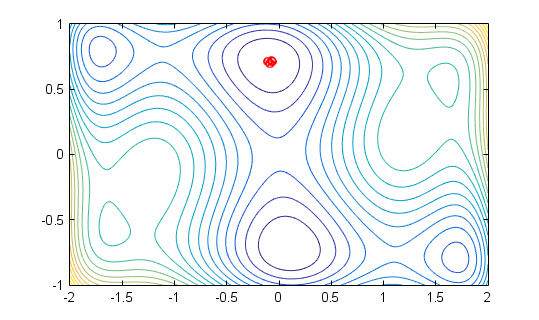
Nelder Mead on 6HCF

Nelder Mead running on 6 Hump Camelback Function

This package provdes implementations for some common numerical optimization algorithms. All algorithms solve an unconstrained minimization over a real vector space.

Usage

To use the Fletcher-Reeves Conjugate Gradient method with Strong Wolfe condition cubic interpolation line search to optimize Rosenbrock's function:

import breeze.linalg._
import breeze.numerics._
import com.feynmanliang.optala.GradientOptimizer
import com.feynmanliang.optala.GradientAlgorithm
import com.feynmanliang.optala.LineSearchConfig

// Define Rosenbrock's function and its gradient
val f: Vector[Double] => Double = v => pow(1D - v(0), 2) + 100D * pow(v(1) - pow(v(0), 2),2)
val gradf: Vector[Double] => Vector[Double] v => {
  DenseVector(
      -2D*(1 - v(0)) - 400D * v(0) * (-pow(v(0), 2) + v(1)),
      200D * (-pow(v(0), 2) + v(1))
      )
}

// Starting point
val x0 = DenseVector(-3D, -4D)

val gradOpt = new GradientOptimizer(maxSteps=3000, tol=1E-6)
val result = gradOpt.minimize(
  f,
  gradf,
  x0,
  GradientAlgorithm.ConjugateGradient,
  LineSearchConfig.CubicInterpoloation,
  reportPerf = true)
println(result)

Installation

In your project's build.sbt

  1. Add Sonatype OSS Snapshots resolver
resolvers +=
"Sonatype OSS Snapshots" at
"https://oss.sonatype.org/content/repositories/snapshots"
  1. Add the dependency
libraryDependencies += "com.feynmanliang.optala" % "optala_2.11" % "0.1.0-SNAPSHOT"

Description

This package currently implements the first order gradient-based methods:

  • Steepest-Descent (GradientAlgorithm.SteepestDescent)
  • Conjugate Gradient with Fletcher-Reeves method (GradientAlgorithm.ConjugateGradient)

To perform line search and choose step size, we currently support:

  • Cubic interpolation with zoom satisfying Strong Wolfe Conditions (LineSearchConfig.CubicInterpoloation)
  • Exact step-size for quadratic forms (GradientOptimizer.minQuadraticForm and LineSearchConfig.Exact))

Additionally, we support the following gradient-free methods:

  • Nelder-Mead
  • Genetic Algorithm

WishList

  • Second order methods (Newtons, LBFGS, etc)
  • More conjugate gradient formulas
  • More line search interpolation methods
  • Conjugate-gradient preconditioning
  • Better reporting of optimization performance stats