You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
I''ve sent you email twice but have not recieved any response. I am not sure if there is any connection problem and I try to connect you via github issues.
I found there might be two mistakes in the paper.
In Eq. 5, the range of S should be (-pi, pi), so I think S should be out of the innermost scope: $A\cdot sin(2pi(F\cdot Tau-S)+B (5) -> A\cdot sin(2pi(F\cdot Tau)-S)+B (5.1) $, or divided by 2pi before passing it in Eq. (5).
I found it hard to predict S to be similar to the curve in fig. 3 using Eq. 5 directly. I tested Eq. (5) and Eq. (5.1) and plotted the figures after training for 5 epoches.
Eq 5:
Eq 5.1:
In Eq 9, the next phase is calculated by interpolating two phases, and multiply it by $A_{t+dt}$:
However, the phase $P_t$ and $P_{t+dt}$ also contains the information about the amplitudes, so the expected prediction of $A_{t+dt}$ should be very similar to one, which means scale the interpolated result. I am not sure if the amplitudes should be predicted by the difference between two frames, just like the frequency does?
Besides, I am not sure how to handle the loss of the phase. I employ the mse loss between the predicted phase in eq 9 and the groundtruth phase, but the frequency of the predicted phase is inaccurate. Do we have to employ loss on the amplitudes and frequence additionally? Which method do you use?
I will appreciate it if you correct me if I am wrong.
I look forward to hearing from you.
Best regards,
Xiangjun Tang
The text was updated successfully, but these errors were encountered:
Hello Sebastian,
I''ve sent you email twice but have not recieved any response. I am not sure if there is any connection problem and I try to connect you via github issues.
I found there might be two mistakes in the paper.
In Eq. 5, the range of S should be (-pi, pi), so I think S should be out of the innermost scope:$A\cdot sin(2pi(F\cdot Tau-S)+B (5) -> A\cdot sin(2pi(F\cdot Tau)-S)+B (5.1) $ , or divided by 2pi before passing it in Eq. (5).

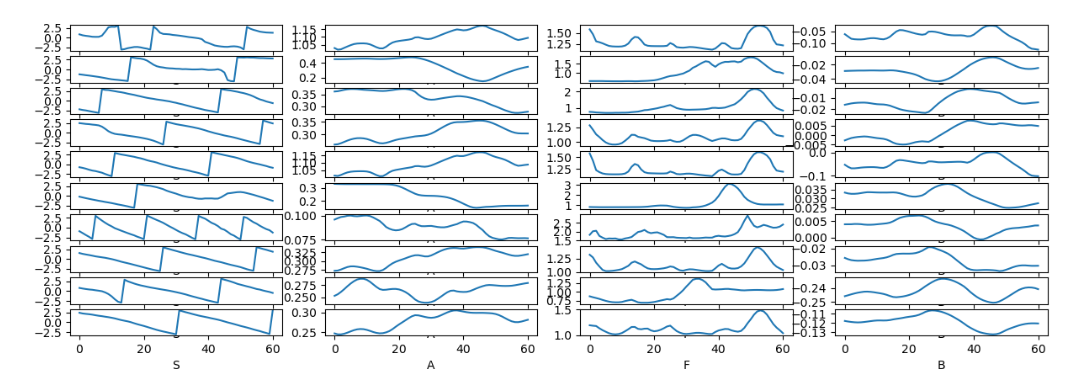
I found it hard to predict S to be similar to the curve in fig. 3 using Eq. 5 directly. I tested Eq. (5) and Eq. (5.1) and plotted the figures after training for 5 epoches.
Eq 5:
Eq 5.1:
In Eq 9, the next phase is calculated by interpolating two phases, and multiply it by$A_{t+dt}$ :

$P_t$ and $P_{t+dt}$ also contains the information about the amplitudes, so the expected prediction of $A_{t+dt}$ should be very similar to one, which means scale the interpolated result. I am not sure if the amplitudes should be predicted by the difference between two frames, just like the frequency does?
However, the phase
Besides, I am not sure how to handle the loss of the phase. I employ the mse loss between the predicted phase in eq 9 and the groundtruth phase, but the frequency of the predicted phase is inaccurate. Do we have to employ loss on the amplitudes and frequence additionally? Which method do you use?
I will appreciate it if you correct me if I am wrong.
I look forward to hearing from you.
Best regards,
Xiangjun Tang
The text was updated successfully, but these errors were encountered: