| 数据结构 | 变种 | 相关题目 | 讲解文章 |
| 顺序线性表:向量 Vector | |||
| 栈和队列 Stack & Queue | 1. 广义表 Generalized List/GList 2. 双端队列 Deque |
||
| 队列 Queue | 1. 链表实现 Linked List Implementation 2. 循环数组实现 ArrayQueue 3. 双端队列 Deque 4. 优先队列 Priority Queue 5. 循环队列 Circular Queue |
||
| 单链表 Singly Linked List | 1. 双向链表 Double Linked Lists 2. 静态链表 Static List 3. 对称矩阵 Symmetric Matrix 4. 稀疏矩阵 Sparse Matrix |
||
| 哈希表 Hash Table | 1. 散列函数 Hash Function 2. 解决碰撞/填充因子 Collision Resolution |
||
| 字符串 String | 1. KMP 算法 2. 有限状态自动机 3. 模式匹配有限状态自动机 4. BM 模式匹配算法 5. BM-KMP 算法 6. BF 算法 |
||
| 树 Tree | 1. 二叉树 Binary Tree 2. 并查集 Union-Find 3. Huffman 树 |
||
| 数组实现的堆 Heap | 1. 极大堆和极小堆 Max Heap and Min Heap 2. 极大极小堆 3. 双端堆 Deap 4. d 叉堆 |
||
| 树实现的堆 Heap | 1. 左堆 Leftist Tree/Leftist Heap 2. 扁堆 3. 二项式堆 4. 斐波那契堆 Fibonacco Heap 5. 配对堆 Pairing Heap |
||
| 查找 Search | 1. 哈希表 Hash 2. 跳跃表 Skip List 3. 排序二叉树 Binary Sort Tree 4. AVL 树 5. B 树 / B+ 树 / B* 树 6. AA 树 7. 红黑树 Red Black Tree 8. 排序二叉堆 Binary Heap 9. Splay 树 10. 双链树 Double Chained Tree 11. Trie 树 12. R 树 |
数组是列表的实现方式之一,也是面试中经常涉及到的数据结构。
正如前面提到的,数组是列表的实现方式,它具有列表的特征,同时也具有自己的一些特征。然而,在具体的编程语言中,数组这个数据结构的实现方式具有一定差别。比如 C++ 和 Java 中,数组中的元素类型必须保持一致,而 Python 中则可以不同。Python 中的数组叫做 list,具有更多的高级功能。
读取数组中的元素,是通过访问索引的方式来读取的,索引一般从 0 开始。
在计算机中,内存可以看成一些已经排列好的格子,每个格子对应一个内存地址。一般情况下,数据会分散地存储在不同的格子中。
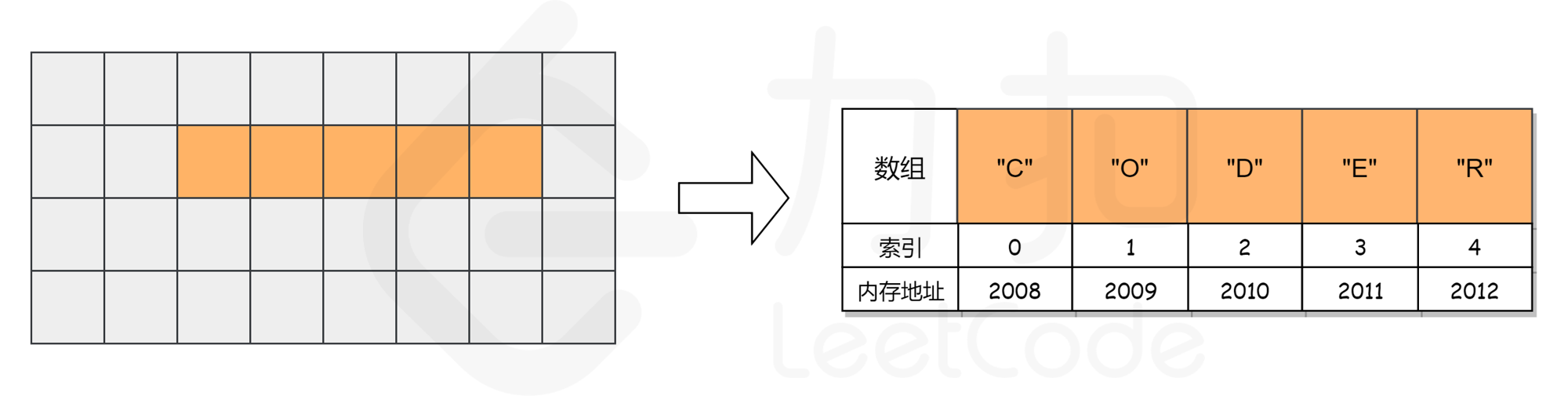
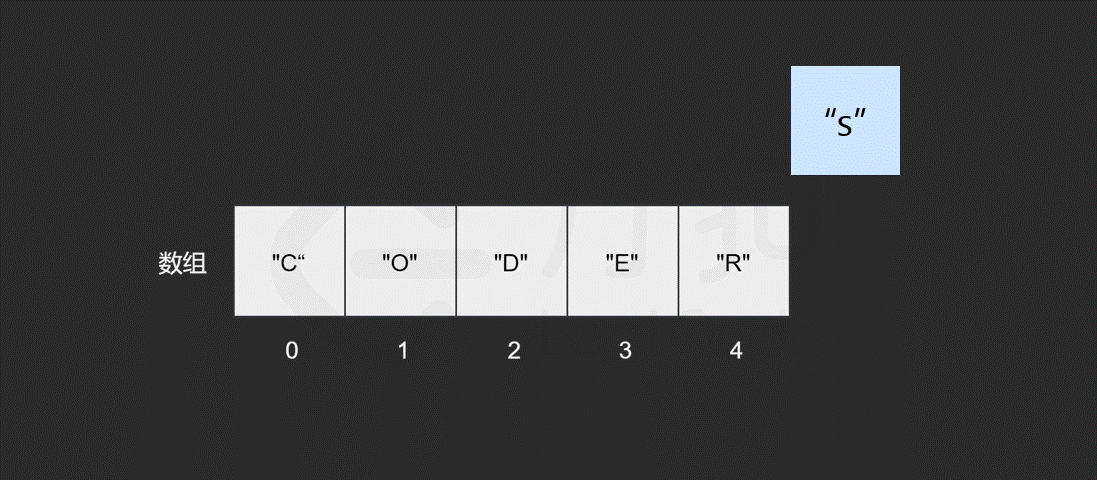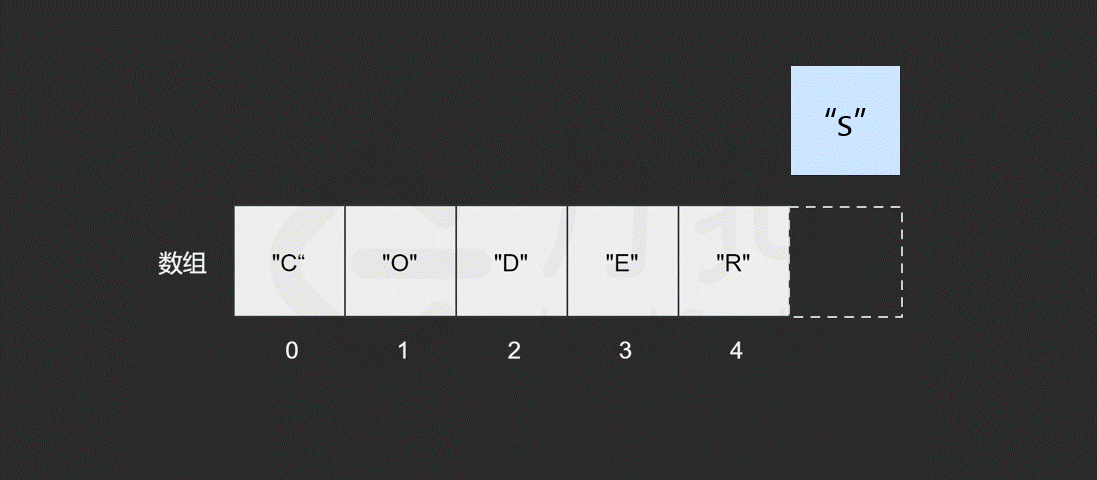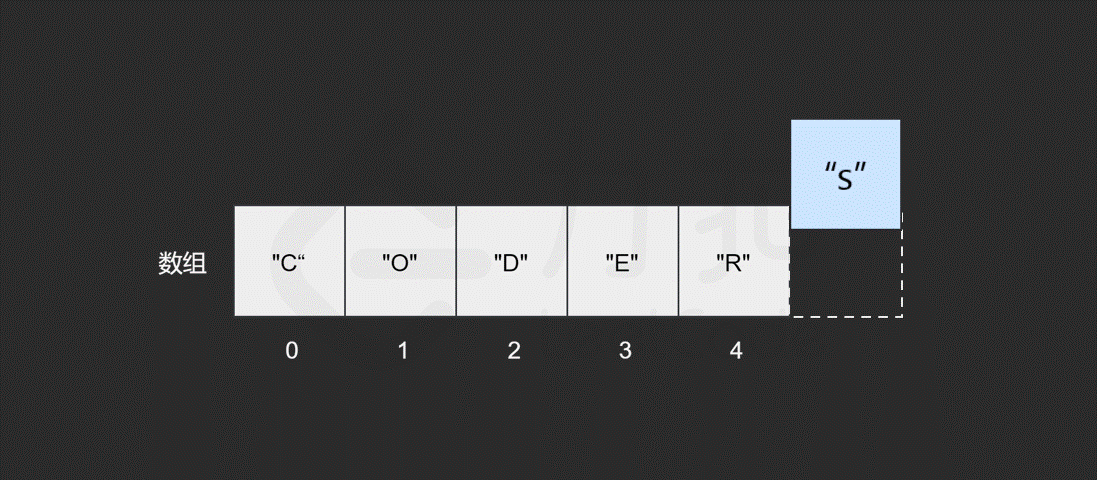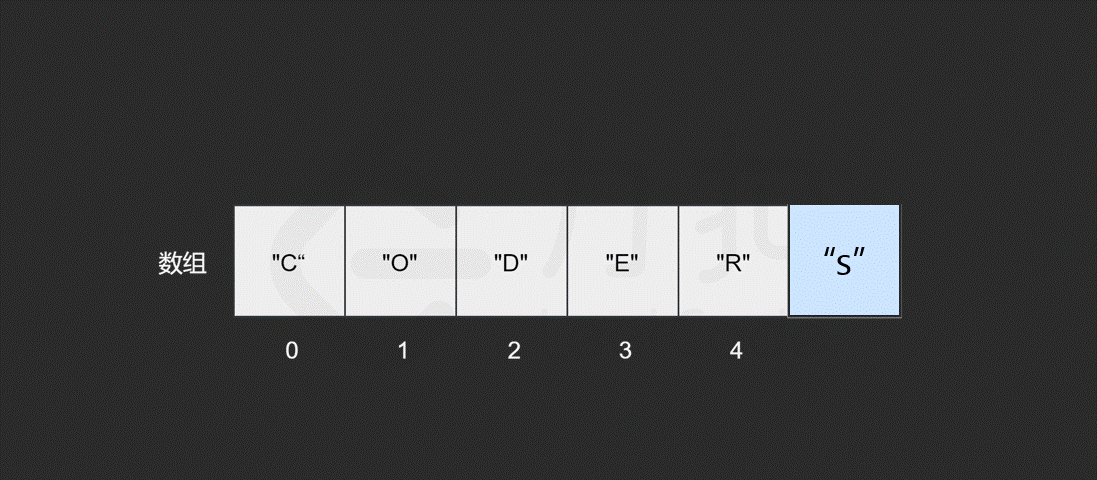
而对于数组,计算机会在内存中为其申请一段 连续 的空间,并且会记下索引为 0 处的内存地址。以数组 ["C", "O", "D", "E", "R"] 为例,它的各元素对应的索引及内存地址如下图所示。
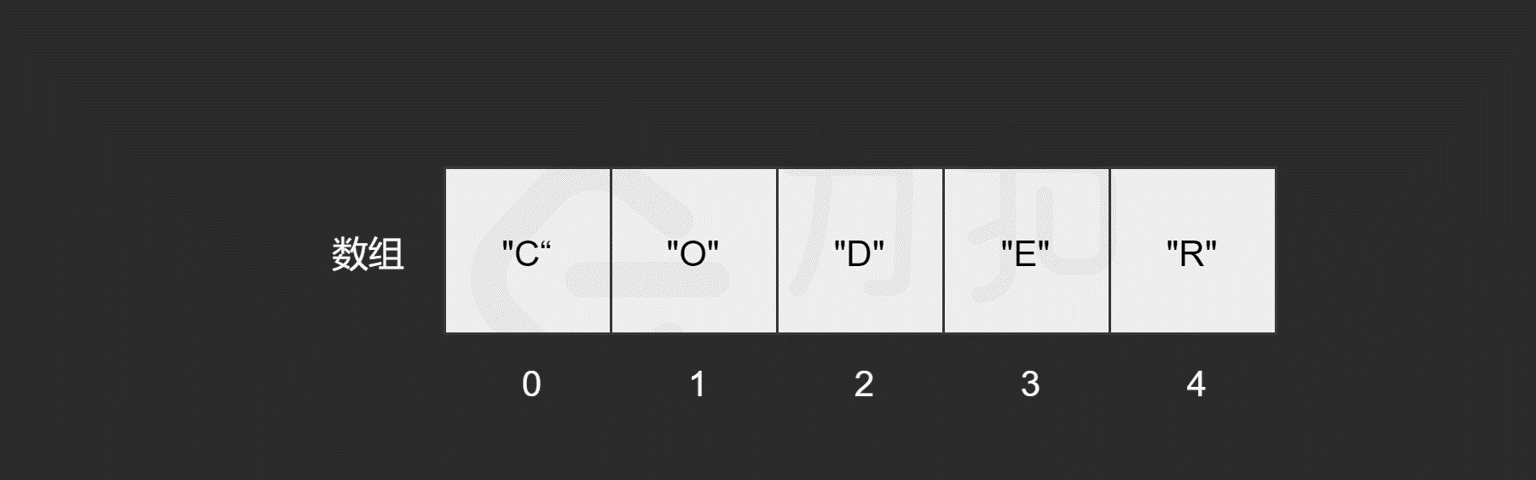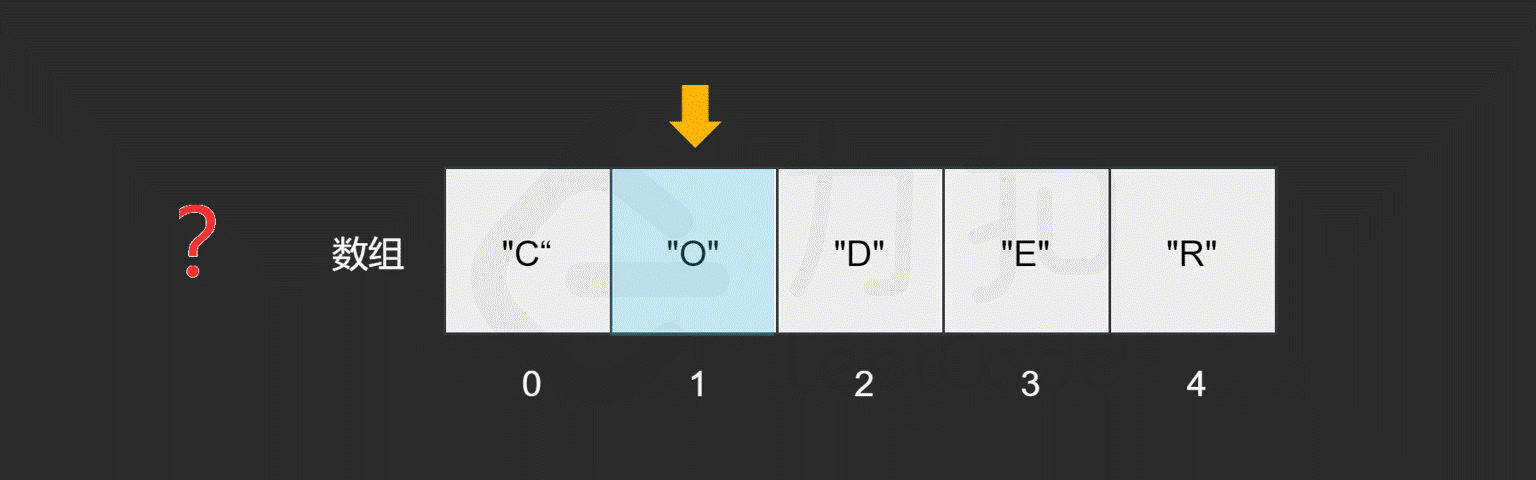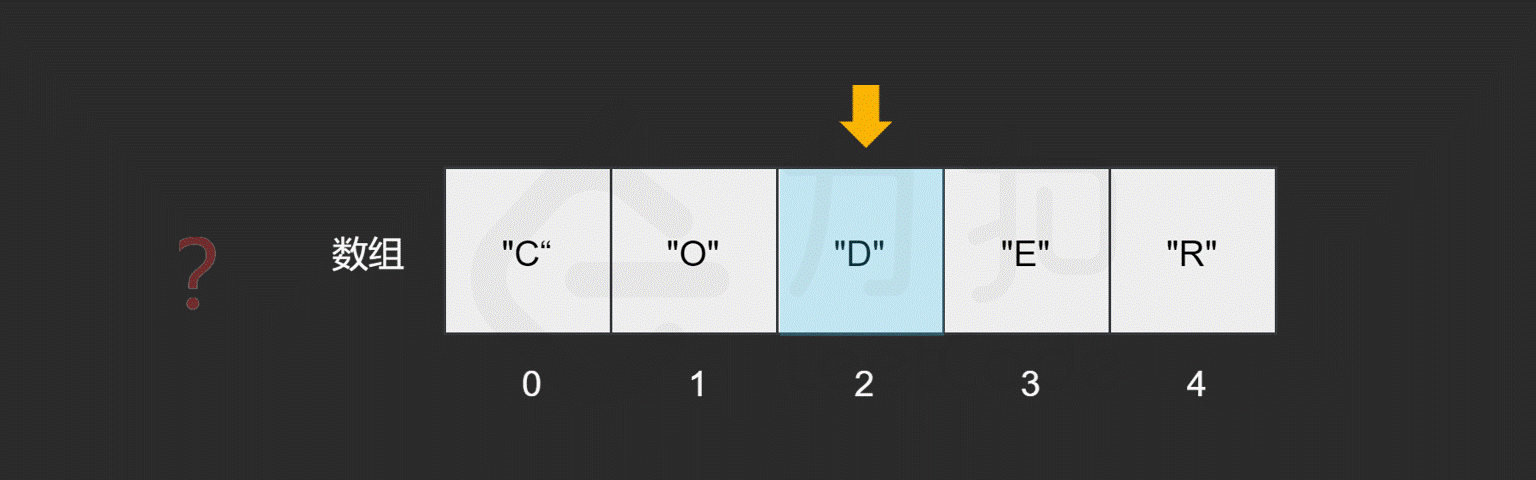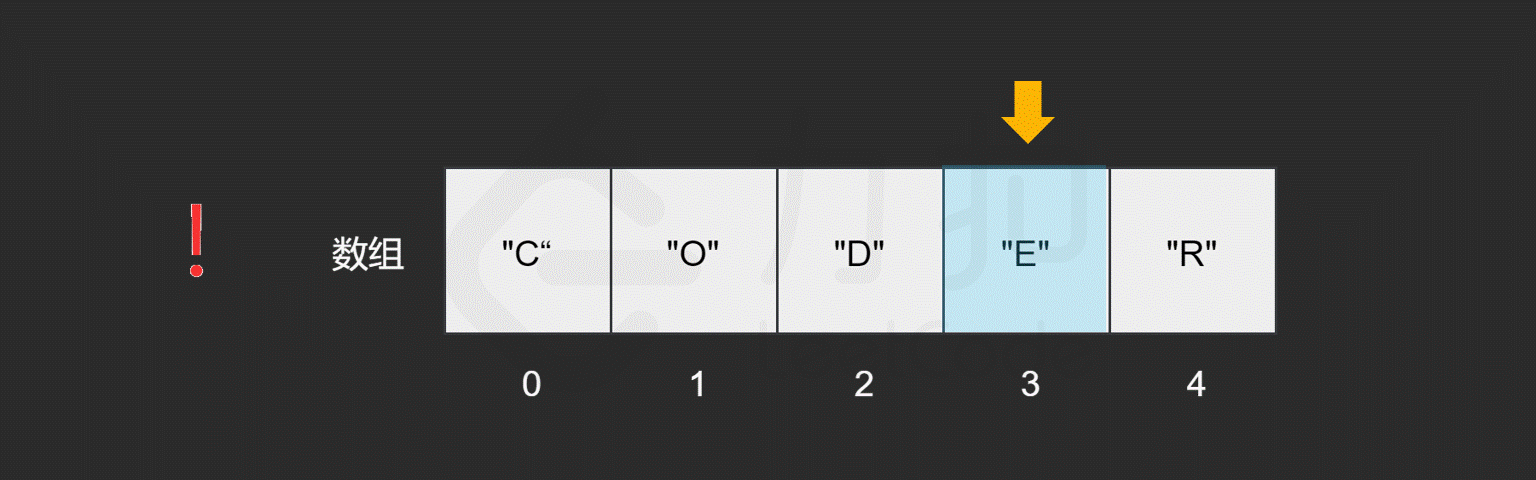
假如我们想要访问索引为 2 处的元素 "D" 时,计算机会进行以下计算:
找到该数组的索引 0 的内存地址: 2008; 将内存地址加上索引值,作为目标元素的地址,即 2008 + 2 = 2010,对应的元素为 "D",这时便找到了目标元素。 我们知道,计算内存地址这个过程是很快的,而我们一旦知道了内存地址就可以立即访问到该元素,因此它的时间复杂度是常数级别,为 O(1)。
假如我们对数组中包含哪些元素并不了解,只是想知道其中是否含有元素 "E",数组会如何查找元素 `"E" 呢?
。
我们发现,最坏情况下,搜索的元素为 "R",或者数组中不包含目标元素时,我们需要查找 n 次,n 为数组的长度,因此查找元素的时间复杂度为 O(N),N。
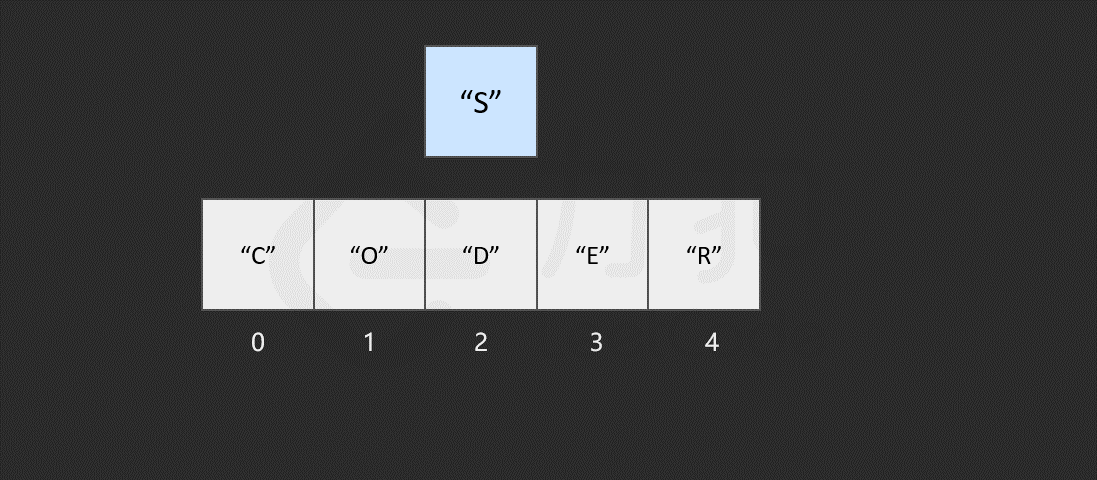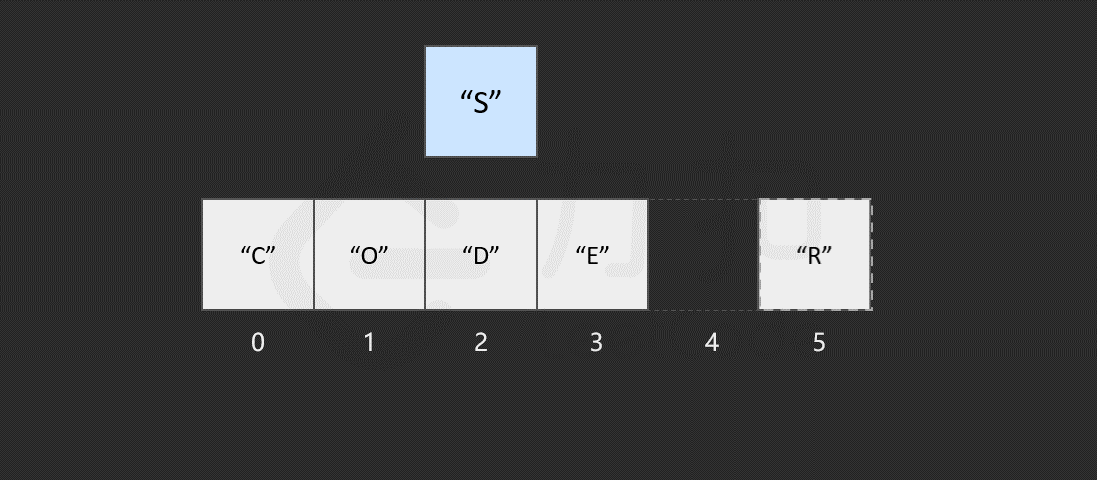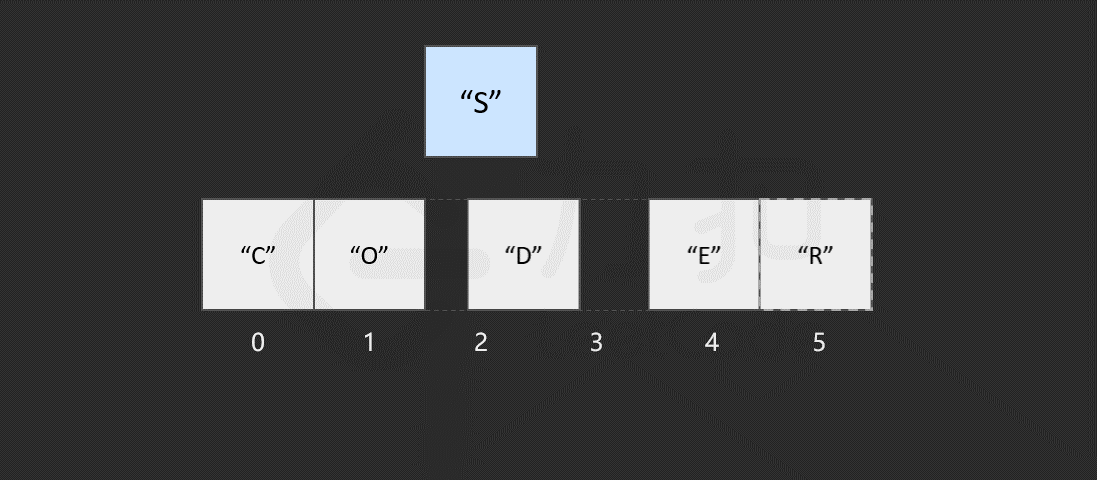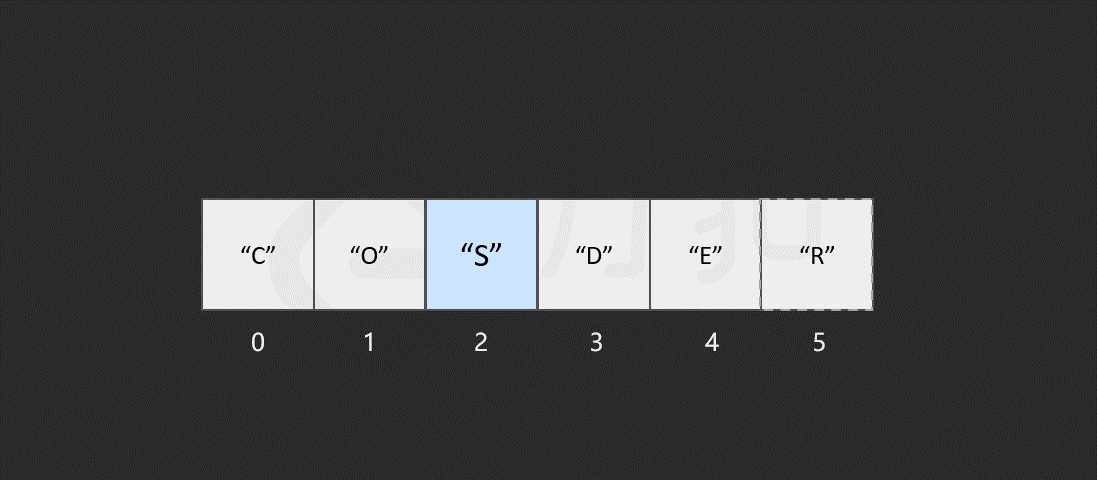
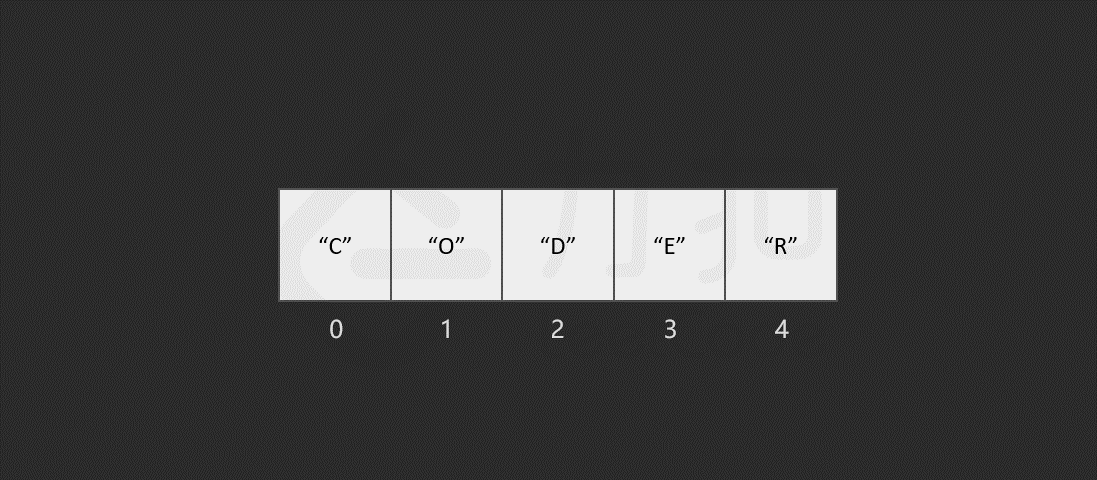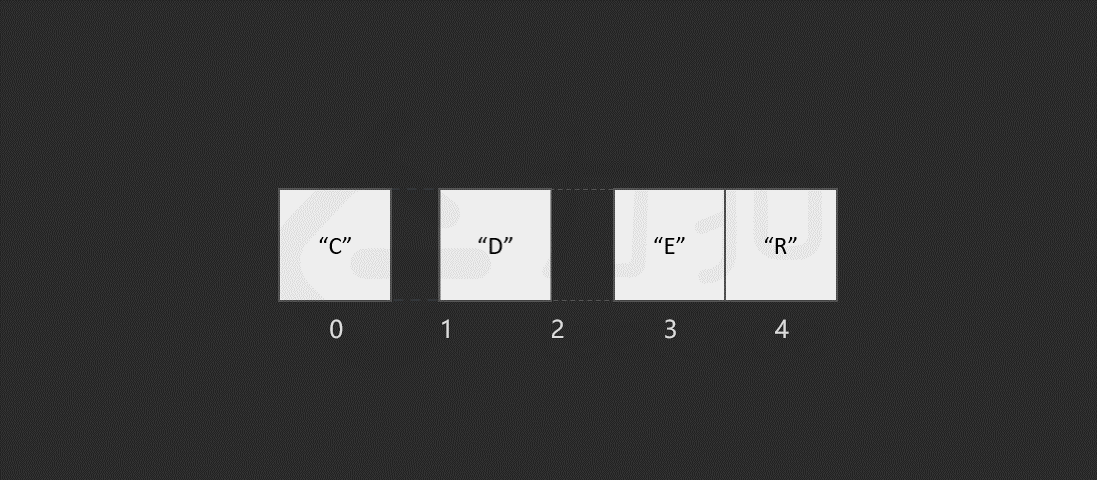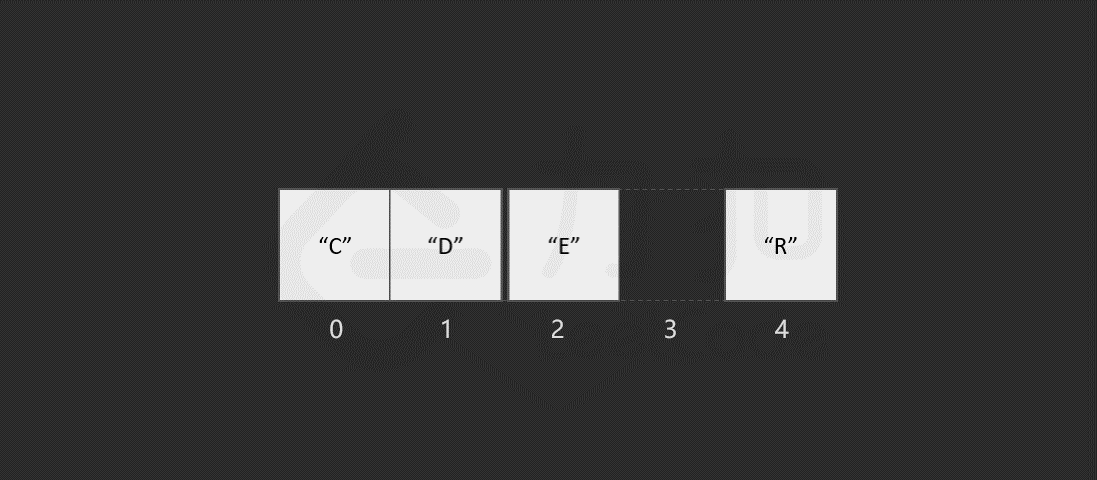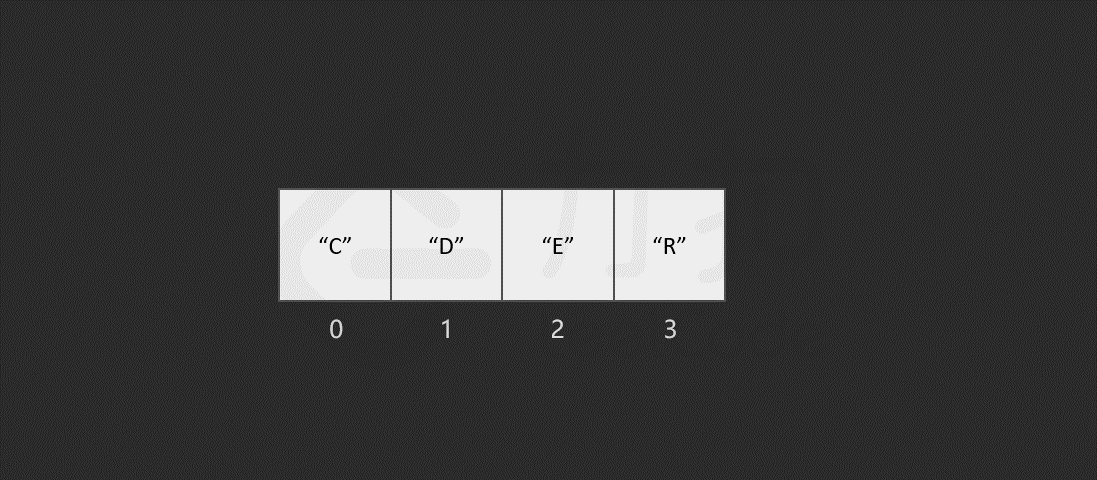
我们发现,如果需要频繁地对数组元素进行插入操作,会造成时间的浪费。事实上,另一种数据结构,即链表可以有效解决这个问题
给定一个整数类型的数组 nums,请编写一个能够返回数组 “中心索引” 的方法。
我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
示例 1:
输入:
nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
索引 3 (nums[3] = 6) 的左侧数之和 (1 + 7 + 3 = 11),与右侧数之和 (5 + 6 = 11) 相等。
同时, 3 也是第一个符合要求的中心索引。
示例 2:
输入:
nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心索引。
说明:
- nums 的长度范围为 [0, 10000]。
- 任何一个 nums[i] 将会是一个范围在 [-1000, 1000]的整数。
相关标签
数组
public class Solution {
public int PivotIndex(int[] nums) {
int leftSum = 0;
int rightSum = nums.Sum();
for (int i = 0; i < nums.Length; i++)
{
if (leftSum == rightSum - leftSum - nums[i])
return i;
leftSum += nums[i];
}
return -1;
}
}给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
相关标签数组 二分查找
public class Solution {
public int SearchInsert(int[] nums, int target) {
int length = nums.Length;
if (nums[length - 1] < target)
{
return length;
}
int left = 0, right = length - 1, mid=0;
while (left < right)
{
mid = left + (right - left) / 2;
if (nums[mid] < target)
left=mid+1;
if (nums[mid] >= target)
right=mid;
}
return left;
}
}给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: intervals = [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间
提示:
- intervals[i][0] <= intervals[i] [1]
相关标签排序 数组
//暴力解法
public static int[][] Merge(int[][] intervals)
{
int m = 0;
while (m < intervals.Length)
{
int n = 0;
while (m==n|| n < intervals.Length&&!(intervals[m][intervals[m].Length - 1] >= intervals[n][0] && intervals[m][0] <= intervals[n][intervals[n].Length - 1]))
n++;
if (n < intervals.Length)
intervals=ChangeArray(intervals, m, n);
else
m++;
}
return intervals;
}
private static int[][] MoveItem(int[][] intervals,int index)
{
while (index != intervals.Length-1)
intervals[index] = intervals[++index];
intervals=intervals.Skip(0).Take(intervals.Length-1).ToArray();
return intervals;
}
private static int[][] ChangeArray(int[][] intervals,int m,int n)
{
int a = 0, b = 0;
if (intervals[m][0] < intervals[n][0])
a = intervals[m][0];
else
a = intervals[n][0];
if (intervals[m][intervals[m].Length - 1] < intervals[n][intervals[n].Length - 1])
b = intervals[n][intervals[n].Length - 1];
else
b = intervals[m][intervals[m].Length - 1];
intervals[m][0] = a;
intervals[m][intervals[m].Length - 1] = b;
intervals = MoveItem(intervals, n);
return intervals;
}//运行速度较快
public static int[][] Merge(int[][] intervals)
{
List<int[]> intList = new List<int[]>();
for (int i = 0; i < intervals.Length; i++)
{
intList.Add(intervals[i]);
}
intList.Sort((a, b) =>
{
return a[0] - b[0];
});
List<int[]> retList = new List<int[]>();
retList.Add(intList[0]);
for (int j = 1; j < intList.Count; j++)
{
if (intList[j][0] <= retList[retList.Count - 1][retList[retList.Count-1].Length - 1])
{
retList[retList.Count - 1][retList[retList.Count - 1].Length - 1] = Math.Max(retList[retList.Count - 1][retList[retList.Count - 1].Length - 1], intList[j][intList[j].Length - 1]);
}
else
retList.Add(intList[j]);
}
return retList.ToArray();
}