...What started off as a new rule or two that could be used to define how to make Polyominoes, turned into slowly building a websoft to just find Omni Shapes (or Polyominoes) in that slightly new way...
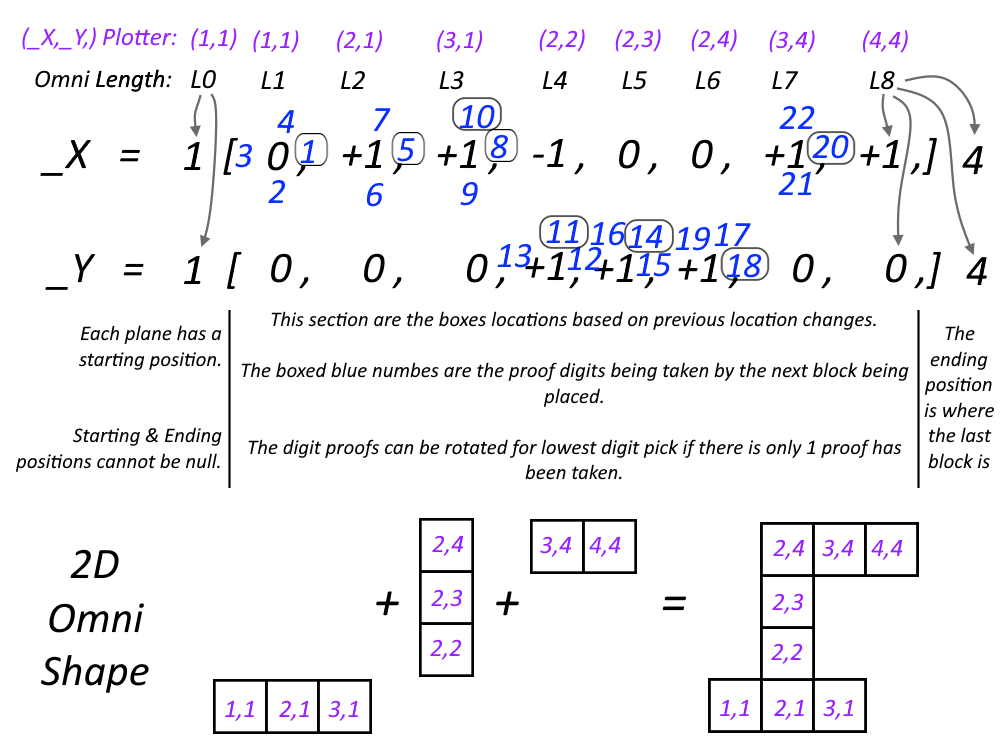
To start, The major thing Omni Shapes does different then Polyominoes is tracking the shapes by relatable coordinates instead of strictly-visual, corner-to-corner binary pairing or matrix based methods. Ideally, we would place our first block in the relatable spot on the graph as to the first block we plan on taking (not placing) then we can track each block's position and backtrack to determine the possible numbers "taken" even after a push (to ensure we don't break the take-place rule used to determine finding Polyominoes). For example if we always place the smallest number at the top of 1st placed block & if I know I'm going to pick the right side block of the first, then I'll place the first block at 4,4 (scale out as your dimensions rise ie: 4,4,4 [3D] && 4,4,4,4 [4D]). Now any move we make we can record the difference from the previous position to the current and this will allow us to track each step. When recording, lead by placing the starting postion then within brackets the changes and outside the brackets the tailing end should be the ending location. This should allow anyone to be able to grab a graph and re-create the shape, also this allows us to find Omni Shape reflections or "free" Polyominoes. A simple reflection is just the opposite sign of the change but we could use an algo to find all free shapes or omni reflections.
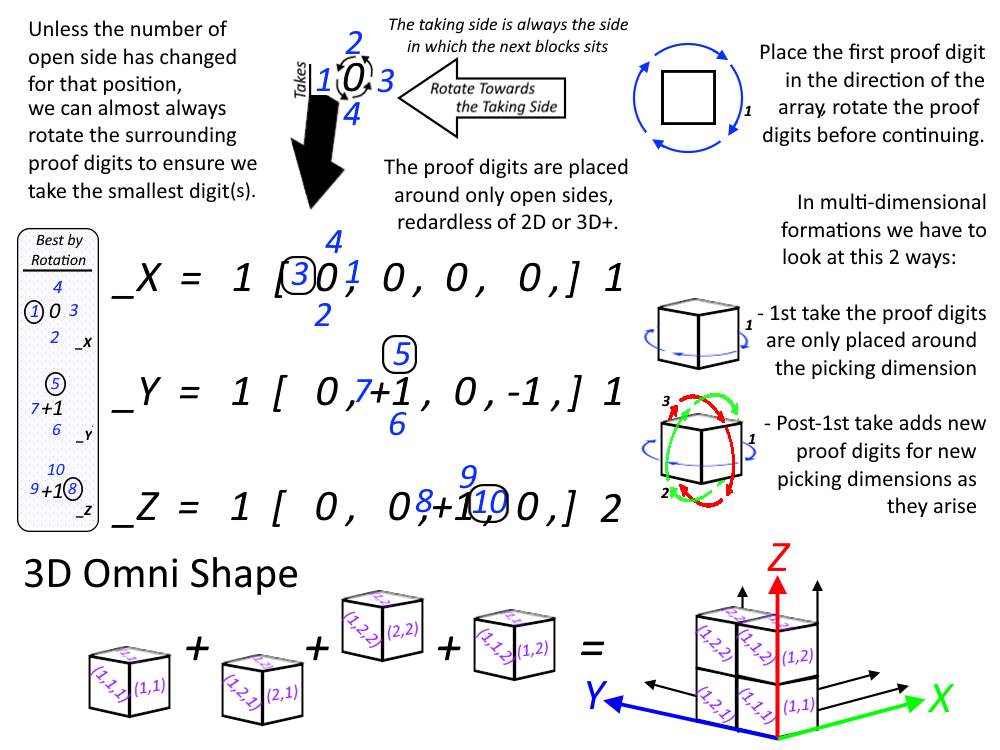
Because we are using corridanates we can take each position of the blocks (by starting at the start and working down the changes to the end) and mathematically or deterministically rotate based on the grid (like rotating a block that has a specific shape on it) ((max-grid-size MINUS grid-position-per-plane) PLUS one) but also we can just flip the X-Y values to create a mirror and in higher deminsions flipping the alpha & delta with x & y should flip the shape inside-out. Now without folding symatry methods nor heavy matrix maths we can find all the Omni's reflections (or "free Polyominoes").
Shapes are their specific pattern in their change arrays. For example: in each change array (x|y|alpha|delta|[...]) we have start[change]end. A real 2D Omni may look like 4[-1,-1,0]2;4[0,0,1]5. It's an "L" type shape that moves 2 times in one direction then moves 90deg off one side for one block, making the total length 4 (or L4). Started at 4,4 ended at 2,5. So the pattern (A,A,B):(B,B,A) is a specific shape and we can then use this as a changeable object. As we find more Fixed Polyominoes or Unique-Patterned Omnis we can hot swap sections with these shape patterns while keeping true to the object before it. If need be we can always do test pushes to see if an addtional set of onjects can be placed around the edges of the object (to detect self & patterns looping around to have holes). Just push for as many times your longest length of the shape is or the length of the non-null objects of the change array with the most non-null objects.
At the moment the Omni Shape Finder doesn't do all the extra steps to finding new moves nor does it use the simple method described above. It's easier to start at Null (0) and change by (0) then build patterns then hot swap the patterns with slow rising changing numbers and slowly rising the length as you find all patterns within a length. Instead the Omni Shape Finder uses video game logic to "look" around and find potential moves, records them then tries to send a clone in it's place to take that potential move.
Example Omni:
X Plane: 4[0,0,0,-1,-1,0,0,0,-1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,-1]8
Y Plane: 4[-1,-1,-1,0,0,1,1,1,0,1,1,1,1,1,0,0,0,0,0,0,0,0,-1,-1,-1,-1,-1,-1,0]3
Z Plane (alpha): 4[1,1,0,0,0,-1,0,0,0,0,1,0,0,0,0,0,0,-1,-1,-1,-1,-1,0,0,0,1,1,0,0]3
Single Array (SA) Formatted: <254:264,X(4[0,0,0,-1,-1,0,0,0,-1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,-1]8),Y(4[-1,-1,-1,0,0,1,1,1,0,1,1,1,1,1,0,0,0,0,0,0,0,0,-1,-1,-1,-1,-1,-1,0]3),Z(4[1,1,0,0,0,-1,0,0,0,0,1,0,0,0,0,0,0,-1,-1,-1,-1,-1,0,0,0,1,1,0,0]3),L30>
3D Omni Shape Mapped (X;Y;Z) Formatted: (4[0,0,0,-1,-1,0,0,0,-1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,-1]8;4[-1,-1,-1,0,0,1,1,1,0,1,1,1,1,1,0,0,0,0,0,0,0,0,-1,-1,-1,-1,-1,-1,0]3;4[1,1,0,0,0,-1,0,0,0,0,1,0,0,0,0,0,0,-1,-1,-1,-1,-1,0,0,0,1,1,0,0]3)
That would be a real 3D Polyomino with 30 blocks (or an L30 Omni)!
Next, I want Omni Shapes to find & make additional pushes avaiable (after the inital algo-push/move) until it's found potientially all shapes per length as the user is clicking to build their Omni Shape. Eventually, I'll probably do the simple line algo across multiple planes (x|y|alpha|delta|[...]) to then mix and match shapes after finding the simplist 13 shapes. Most likely I'll use the tricks I used with SPX to help make that happen. ;}
Try Omni Shapes (websoft) vis-a-vis gisthub preview: 3dd.in/Omni
For anyone whom wants to try the simplified array-attack method for finding Omnis, please try the "Simple Omni Game" HTML file.
3D's Note:
The move explination image is no longer completely accurate, the move rules image may be updated soon. Next will be images and hopefully eventually a rule set to help others find more Omni Shapes which are just a different way to look at Polyominoes! (The name Omni comes from me unable to say "Polyomino" so when I attempt to say the same word it comes out, "Poly-Omni-O", but I continued to call them Omni Shapes as I discovered these "Between Complexity Topologies" (my perspective on what are Polyominoes) can create almost any shape.
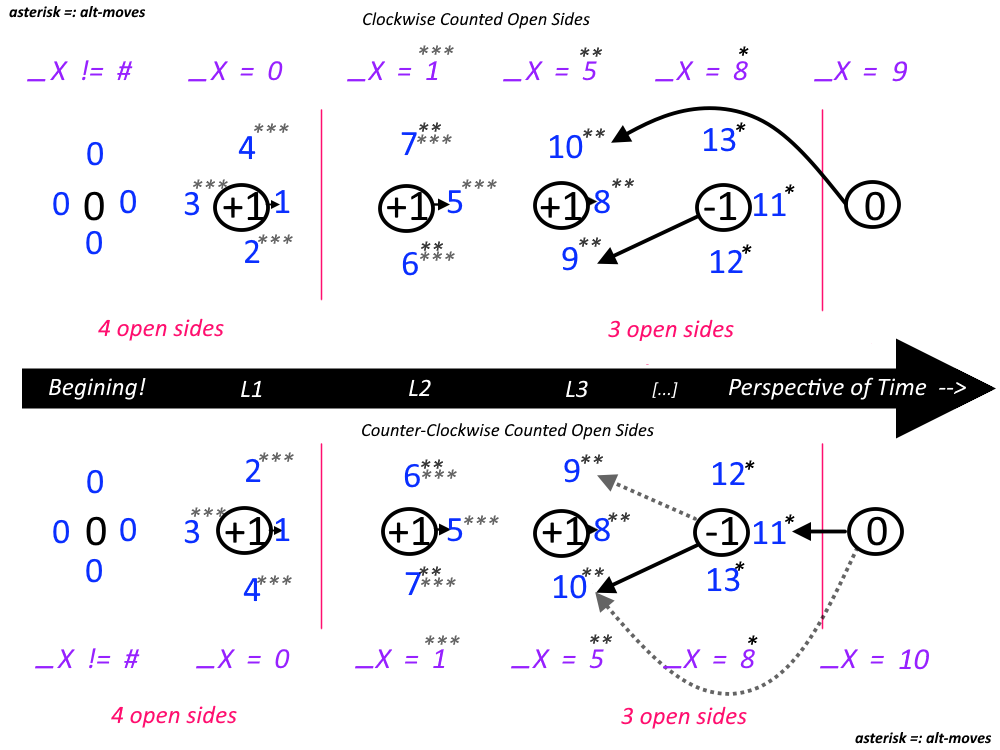
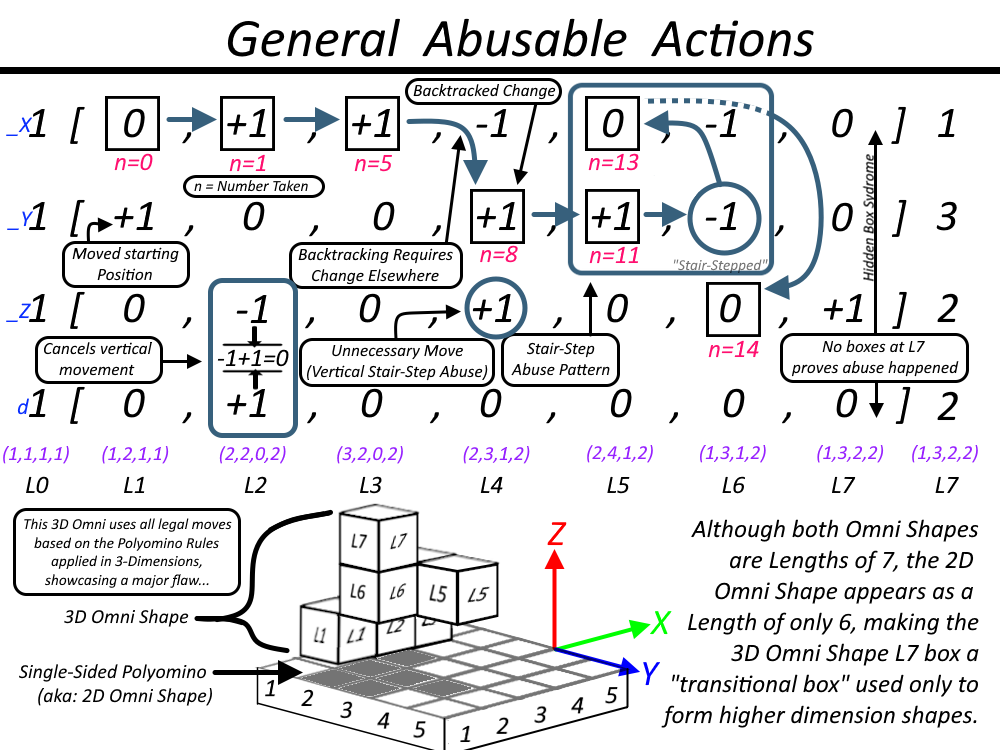
Proof digits are used to track to the open sides during the time of selecting a new block to be placed, but this also limits where future blocks can be placed since we cannot take a proof digit lower than the previous taken proof digit. This is not a unique rule, it is the Polyomino base rule. We add uniquiness to this rule by adding if you are using more then 2 dimentsions you only need to add a new set of proof digits when approaching a previously used block at a new dimension. We can also safely assume the first move is always the lowest possible number since only if we reuse a block (depending on it's _Z and distance from edge or distance from last major change) does it matter which number we take & until we approach the same block a third time does it matter which number have taken because we can always rotate the proof digits or place them in the oppositie direction to ensure we always have the lowest 2 digits avaiable at time of taking. The proof digits only prevent us from moving too far away from any one spot, backtracking to anywhere (forcing us to stay in a direction) but this also create boundary limitors not seen in any other format to find Polyominoes (or at least form 3Douglas' perspective). The proof numbers take a spot, first come first serve. When appraoching an area with a spot taken and the numbers are lower than currently have taken, this creates a boundary where those numbered locations cannot be taken. They are repsctively "out-of-bounds". Using any currently used method to find polyominoes in a mathematical manner does not account for this. The split array method (Simple Omni Game) and game-map methods (Omni Shape Finder) both account for this.
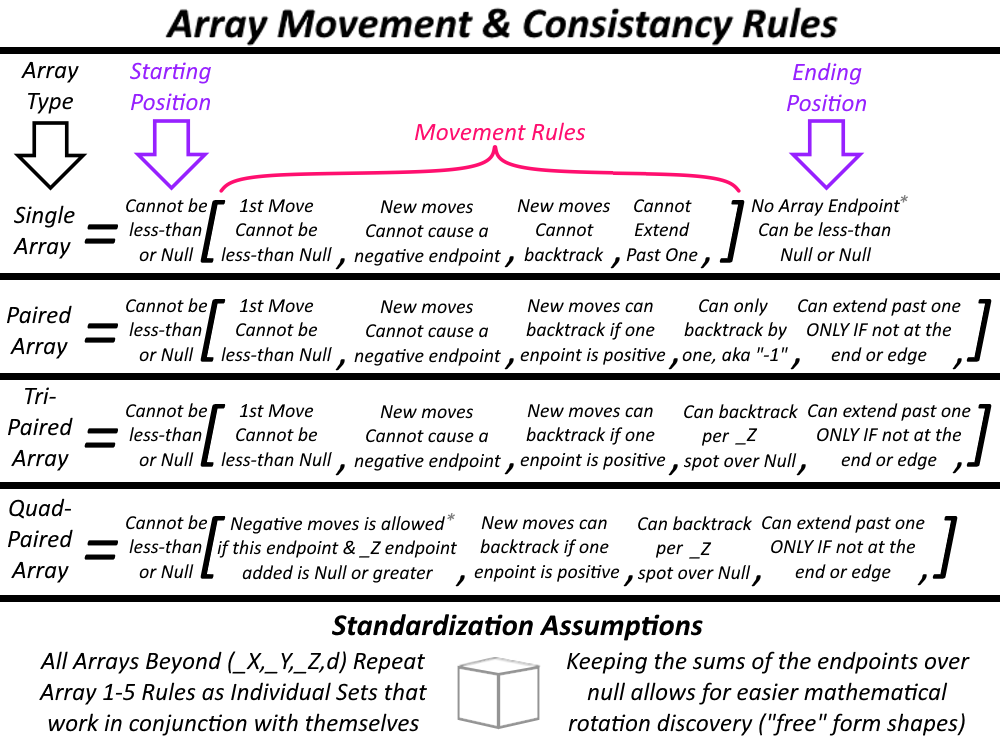
Other rules may be usable depending on if the array is paired or not. Next will be paired-type rules for the Split Array Method (Simple Omni Game):
- The Starting Position cannot be negative (or less than null) nor null ["0"].
- 1st Move cannot be less-than null (negative).
- New Moves cannot cause a negative endpoint.
- New Moves cannot extend past one.
- Ending Position cannot be less then null nor null.
- Starting Position cannoto be less-than null nor null.
- 1st Move cannot be less-than null.
- New Moves cannot cause a negative endpoint.
- Can Backtrack ONLY by ONE ["-1"].
- Can Extend Past One ONLY IF NOT AT an end or edge.
- Endpoints cannot be less-than null nor null.
- Starting Position cannot be less-than null nor null.
- 1st Move cannot be less-than null.
- New moves can cause one of the three endpoints to become negative for as long as the other two endpoints are positive.
- New moves can backtrack by one if all other endpoints are positive, even if it causes this endpoint to be negative but not null.
- Can backtrack per the length of a trailing value minus one if all other endpoints are positive, even if it causes this endpoint to be negative but not null.
- Can retrack back to positive for as long as no endpoint is null & at least 2 other endpoints are positive & we are not extending further than one past an end or edge.
- Can extend past one ONLY IF NOT AT an end or edge.
- Can extend past one ONLY IF NOT AT an end or edge.
- The Starting Position cannot be negative (or less than null) nor null ["0"].
- Negative moves are allowed if this endpoint PLUS _Z endpoint is Null or greater.
- New moves can backtrack per the length of a trailing value minus one if all other endpoints are positive, even if it causes this endpoint to be negative.
- Can extend past one ONLY IF NOT AT an end or edge.
- This endpoint can only be negative if at least 2 of the other endpoints are positive.
Array Consistency & Movement Rules (outside of Polyomino Rules, for keeping consistency across multiple dimensions) (img):
General Abusable Actions (showcases actions some may call improper but does follow the Polyomino Rules & Multi-Dimensional Conesistency Rules) (img):
