Понятия, необходимые для выполнения задания:

• Евклидова плоскоть
• Бинарное дерево поиска
• Итератор

Данные

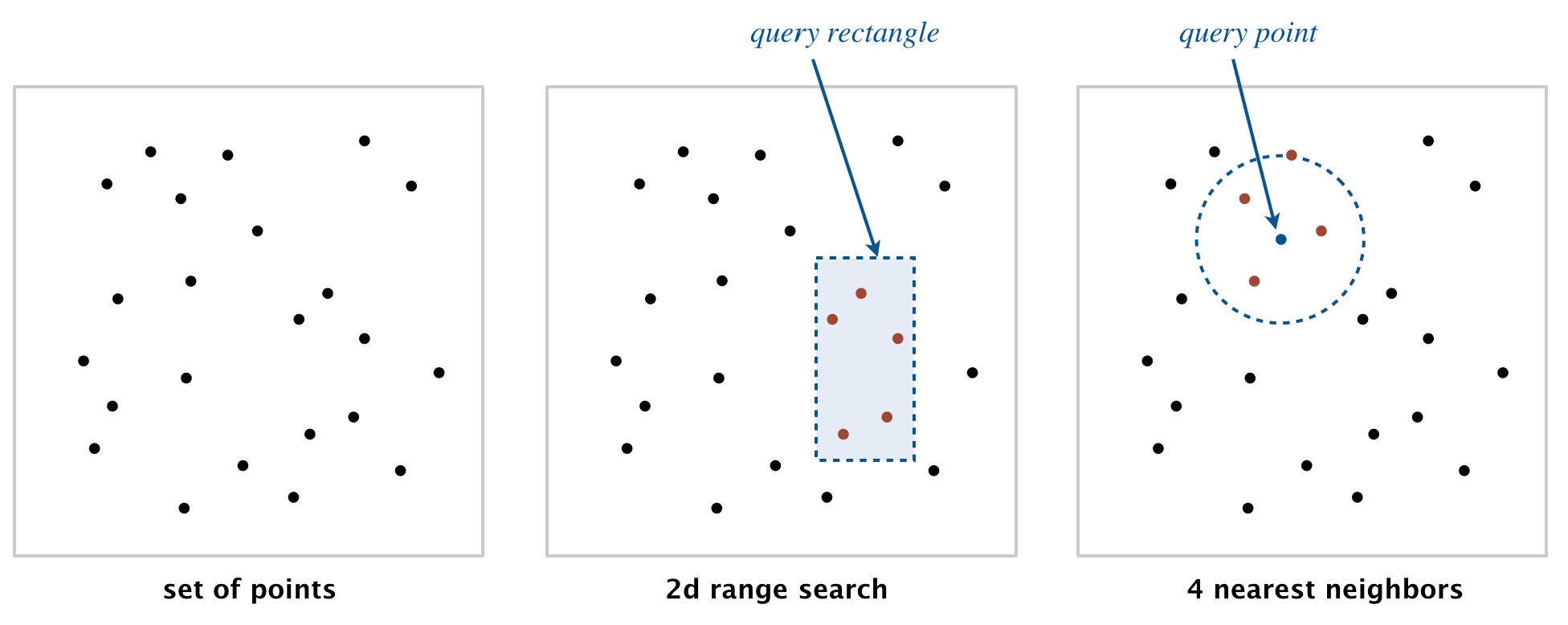
На двумерной евклидовой плоскости расположены N точек.

Задача 1

Дан произвольный прямоугольник (x0, y0), (x1, y1). Из N точек необходимо выбрать все точки, которые попали внутрь этого прямоугольника.

Задача 2

Дана произвольная точка А (xA, yA). Из N точек необходимо найти ближайшую к А точку.

Требования к реализации

Для решения задач необходимо реализовать класс для хранения точек на плоскости:

class PointSet {
public:

    class iterator
    {
	using iterator_category	= std::forward_iterator_tag;
	// To do
    };

    PointSet(const std::string filename = {});

    bool empty() const;

    std::size_t size() const;
    void put(const Point &);
    bool contains(const Point &) const;

    // second iterator points to an element out of range
    std::pair<iterator, iterator> range(const Rect &) const;

    iterator begin() const;
    iterator end() const;

    std::optional<Point> nearest(const Point &) const;
    friend std::ostream & operator <<(const PointSet&);
};

А также классы Point и Rect:

class Point {
public:

	Point(double x, double y);

	double x() const;
	double y() const;
	double distance(const Point &) const; // euclidian distance

	bool operator< (const Point &) const;
	bool operator> (const Point &) const;
	bool operator<= (const Point &) const;
	bool operator>= (const Point &) const;
	bool operator== (const Point &) const;
	bool operator!= (const Point &) const;
};

class Rect {
public:

	Rect(const Point & left_bottom, const Point & right_top);
   
	double xmin() const;
	double ymin() const;
	double xmax() const;
	double ymax() const;
	double distance(const Point &) const;

	bool contains(const Point &) const;
	bool intersects(const Rect &) const;
};

Шаг 1

Используйте реализацию красно-чёрных деревьев из стандартной библиотеки(std::map, std::set) для реализации PointSet. Требования по производительности:

1. Сложность методов PointSet::put(const Point &) и PointSet::contains(const Point &) должна быть О(logN)
2. Сложность методов PointSet::nearest(const Point &) и PointSet::range(const Rect &) должна быть O(N)

Шаг 2

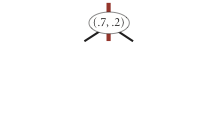
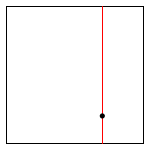
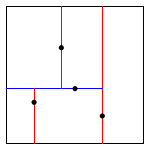
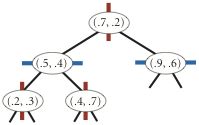
Реализуйте 2-d дерево (Kd tree). 2-d дерево это способ организации дерева поиска двумерных данных. Будем строить 2-d дерево на базе бинарного дерева поиска. Преимуществом организации 2-d дерева является возможность эффективно реализовать поиск точек в заданном прямоугольнике и поиск точки, ближайшей к заданной. Узлом 2-d дерева является точка на плоскости (x, y). При построении 2-d дерева сравнение нового узла (x1, y1) с текущим узлом (x, y) производится либо по координате x, либо по координате y, в зависимости от глубины узла в дереве. Корневой узел -- сравнение по X, узлы глубины 1 -- сравнение по Y, узлы глубины 2 -- сравнение по X, узлы глубины 3 -- сравнение по Y, и т.д.

Пример

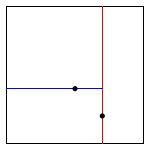
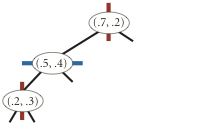
Добавление точки (0.7, 0.2)

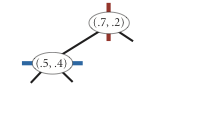
Добавление точки (0.5, 0.4)

Добавление точки (0.2, 0.3)

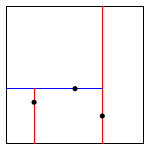
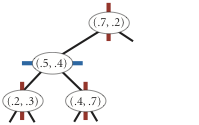
Добавление точки (0.4, 0.7)

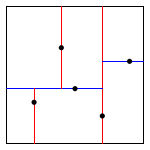
Добавление точки (0.9, 0.6)

Поиск точек, попавших в заданный прямоугольник. В эффективной реализации не следует рассматривать поддеревья, если соответствующий интервал прямоугольника (по X или Y) не пересекается с интервалом поддерева.

Поиск точки, ближайшей к заданной A(x, y). При обходе дерева необходимо хранить текущую наиближайшую точку Z (x0, y0), d = distance(A, Z). Если расстояние от прямоугольника поддерева больше, чем d, то это поддерево можно исключить из обхода. В эффективной реализации обхода дерева сначала следует выбирать то поддерево, в которое могла бы попасть точка A при добавлении в дерево.

Шаг 3

Реализуйте std::pair<iterator, iterator> PointSet::nearest(const Point & x, std::size_t k) const; для поиска k ближайших к заданной точке x точек на плоскости.

Примечания

• PointSet::begin() должен реализовывать обход дерева в глубину.
• Сбалансированность 2d дерева зависит от порядка добавления вершин-точек в дерево. На вход программы поступают точки в произвольном порядке, не гарантирующем построение сбалансированного 2d дерева.
• Предложенные интерфейсы классов Point, Rect и PointSet можно расширять, но нельзя изменять. Введение дополнительных пользовательских типов данных не ограничено.
• Данные могут быть загружены либо передачей файла в конструктор PointSet::PointSet(const std::string & filename), либо с помощью PointSet::put(Point). Формат файла: две колонки, координата X точки и координата Y точки, колонки разделены пробелом. Пример:

0.753 0.943
0.225 0.671
0.763 0.03
0.725 0.338
0.183 0.066

Способ выполнения задания

Задание следует выполнять последовательно: сначала реализовать Шаг 1, затем Шаг 2 и Шаг 3. После каждого шага следует запускать тесты и проверять работоспособность текущей программы.

Производительность решения на базе 2d дерева должна быть на практике лучше, чем производительность решения на базе красно-черного дерева.