-
Notifications
You must be signed in to change notification settings - Fork 122
The NEPO language
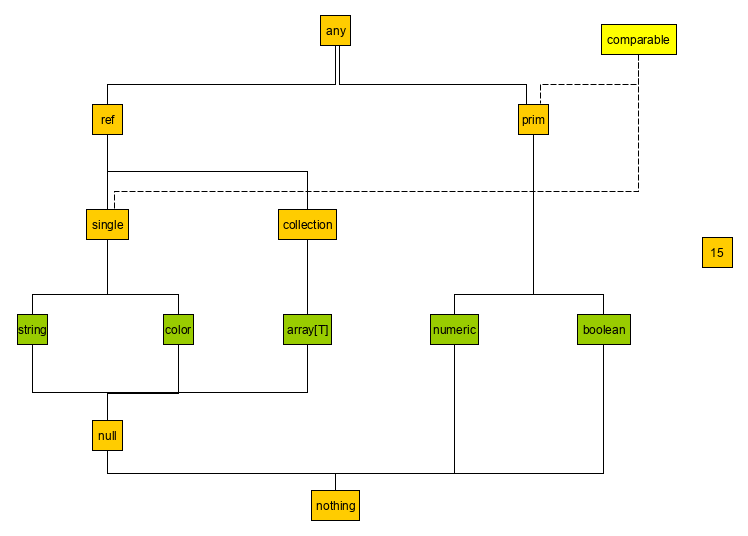
Fig.1 shows the type hierarchy. Notes:
- our simple type system cannot be extended by new types. It is closed.
- the arcs denote the is-a hierarchy between types, e.g. the string type is a ref type and an any type
-
anyis supertype of all types,nothingis subtype of all types. -
refexpresses, that entities of this type are referred to by references (pointers). -
primexpresses, that entities of this type are referred to directly by their values. -
voidis written, if no type is needed, e.g. for function that return no values. -
nullis subtype of all reference types (String and Color). There exists one entity of this type, namednull.
All entities (variables, parameters, constants) have a type. Types define, how entities can be used in functions, and how constants
(literals) of these types look like. For instance, entities of the numeric type can be added or multiplied. A type is selected
by a programmer explicitly, if a variable or a parameter (of a programmer-defined function) is defined. The "green" types from Fig.1 can be
selected explicitly. A type is derived implicitly, if a constant is used, for instance 5 (is of type numeric) or "5" (is of type string).
Constants exist for all "green" types in Fig.1.
- The functions, that can be applied to entities of the various types, are defined below. Each function has a signature, that defines, which entities of what types are expected as parameters and what the type of the entity returned is (if any ...).
- T is used as type parameter.
list[T]is a parametrized type,list[string]is a concrete type. In a program only concrete types can be used, in signatures type parameter are legal. If a function has type variables in its signature, the type parameter must be instantiated to concrete types consistently. E.g.:-
list[T]has methodgetwith signature(idx: numeric) => T. If variablea1is of typelist[string], thena1.get(3)will returnstring, because T is instantiated to string. - the function
==has signature(e1: T,e2: T) => boolean. Thus3==5is correct, but3=="5"is wrong, becauseTmust be instantiated consistently at both places to be either numeric or string.
-
The types comparable[T] and addable[T] are "marker" types, that express, that these types can be used in function that expect these
types as parameters.
The type string is a subtype of comparable[string] and addable[string]. A string constant is written "content-of-the-string"
The type color is a subtype of comparable[color] (note, that the type is not available for all robots). A constant is written
- either
color(COLOR), whereCOLORis gray, grey, red, orange, yellow, green, blue, dark blue, or purple; - or
rgb(r: numeric, g: numeric, b: numeric, sat: numeric) => colorwith numeric values 0<=v<=255 for the red, green, blue and saturation.
The type list[T] is a list. The first item has index 0. Functions makeEmpty*List() => list[T] creates an empty list where ** may be one of
the green types of Fig.1, but no array type. The result type depends in the obvious way on *.
Function makeList(e1: T, ..., en:T) => list[T] creates a list of concrete type array[T] with the items given as parameters and T instantiated
to the (identical) concrete type of the parameters.
The type boolean has constants written as true or false
The type numeric has constants written as 42, -1951, 1.5, 1.5e-23 and so on.
Functions are described in groups for a better overview.
The group equal consists of the functions ...
-
e1 == e2sig(e1: T, e2: T) => boolean. Returns true, if the values of e1 and e2 are equal. Arrays are equal, if they have the same size and all items are equal in turn. -
e1 != e2sig(e1: T, e2: T) => boolean. Inverse of equals.
The group comparable has the functions ...
-
e1 < e2sig(e1: comparable[T], e2: comparable[T]) => boolean. Returns true, if the value of e1 is less than the value of e2. -
e1 <= e2sig(e1: comparable[T], e2: comparable[T]) => boolean. Less equal. -
e1 > e2sig(e1: comparable[T], e2: comparable[T]) => boolean. Greater than. -
e1 >= e2sig(e1: comparable[T], e2: comparable[T]) => boolean. Greater equal.
The group addable has only one function ...
-
e1 + e2sig(e1: addable[T], e2: addable[T]) => T. Adds the parameters, if T is numeric, and concatenates strings, if T is string. Everything else is an error.
The group arithmetic has the function from addable and ...
-
- nsig(n: numeric) => numeric. Negate n. -
n1 - n2sig(n1: numeric, n2: numeric) => numeric. Subtract. -
n1 * n2sig(n1: numeric, n2: numeric) => numeric. Multiply. -
n1 / n2sig(n1: numeric, n2: numeric) => numeric. Divide. -
n1 ^ n2sig(n1: numeric, e2: numeric) => numeric. n1 to the power of n2. -
sqrt(n)sig(n: numeric) => numeric. square root. -
ln(n)sig(n: numeric) => numeric. log to base n. -
e(n)sig(n: numeric) => numeric. e to the power of n. -
10 ^ nsig(n: numeric) => numeric. 10 to the power of n. -
sin(n)sig(n: numeric) => numeric. sin of n. -
cos(n)sig(n: numeric) => numeric. cos of n. -
tan(n)sig(n: numeric) => numeric. tan of n. -
asin(n)sig(n: numeric) => numeric. asin of n. -
acos(n)sig(n: numeric) => numeric. acos of n. -
atan(n)sig(n: numeric) => numeric. atan of n. -
pisig() => numeric. constant pi (3.14159...). -
esig() => numeric. constant e (2.718...). -
phisig() => numeric. constant golden ratio (1.61...). -
sqrtTwosig() => numeric. square root of 2 (1.414...). -
sqrtHalfsig() => numeric. square root of 1/2 (0.7071...). -
isEven(n)sig(n: numeric) => boolean. is n an even number? -
isOdd(n)sig(n: numeric) => boolean. is n an odd number? -
isPrime(n)sig(n: numeric) => boolean. is n a prime? -
isWhole(n)sig(n: numeric) => boolean. is n a whole number? -
isPositve(n)sig(n: numeric) => boolean. is n a positive number? -
isNegative(n)sig(n: numeric) => boolean. is n a negative number? -
isDivisibleBy(m,n)sig(m: numeric, n: numeric) => boolean. is m divisible by n? -
round(n)sig(n: numeric) => numeric. round n up if fraction >= 0.5, else down -
roundUp(n)sig(n: numeric) => numeric. round n up -
roundDown(n)sig(n: numeric) => numeric. round n down -
remainder(m,n)sig(m: numeric, n: numeric) => numeric. return the remainder, if m is divided by n m by n? -
limit(m,f,t)sig(m: numeric, f: numeric, t: numeric) => numeric. return m limited to the values f and t, including. -
random(f,t)sig(f: numeric, t: numeric) => numeric. return a whole random number between the limits f and t, including. -
random()sig() => numeric. return a random number between 0.0 and 1.0, including. -
incr(m,n)sig(m: numeric, n: numeric) => void. increment m by n?
the group logic has the functions ...
-
! bsig(b: boolean) => boolean. Invert b. -
b1 && b2sig(b1: boolean, b2: boolean) => boolean. b1 and b2. b2 is not evaluated, if b1 is false. -
b1 || b2sig(b1: boolean, b2: boolean) => boolean. b1 or b2. b2 is not evaluated, if b1 is true. -
b ? e1 => e2sig(b: boolean, e1: T, e2: T) => T. If b evaluates to true, evaluate and return e1, else e2.
the group list has the functions ...
-
length(l)sig(l: list[T]) => numeric. Return the length of the list. -
isEmpty(l)sig(l: list[T]) => boolean. Return true, if the list is empty, false otherwise. -
searchFirst(l,s)sig(l: list[T], s: T) => numeric. Return the index of the first occurence of s in l, return -1 if not found. -
searchLast(l,s)sig(l: list[T], s: T) => numeric. Return the index of the last occurence of s in l, return -1 if not found. -
get(l,i)sig(l: list[T], i: numeric) => T. Return the element at index i from list l. Undefined behavior, if index does not exist. -
getFromEnd(l,i)sig(l: list[T], i: numeric) => T. Return the element at index length(l)-1-i in list l. Undefined behavior, if index does not exist. -
getFirst(l)sig(l: list[T]) => T. Return the first element from list l. Undefined behavior, if that does not exist. -
getLast(l)sig(l: list[T]) => T. Return the last element from list l. Undefined behavior, if that does not exist. -
getAndRemove(l,i)sig(l: list[T], i: numeric) => T. Remove and return the element at index i from list l. Undefined behavior, if index does not exist. -
getFromEndAndRemove(l,i)sig(l: list[T], i: numeric) => T. Remove and return the element at index length(l)-1-i from list l. Undefined behavior, if index does not exist. -
getFirstAndRemove(l)sig(l: list[T]) => T. Remove and return the first element from list l. Undefined behavior, if that does not exist. -
getLastAndRemove(l)sig(l: list[T]) => T. Remove and return the last element from list l. Undefined behavior, if that does not exist. -
remove(l,i)sig(l: list[T], i: numeric) => T. Remove the element at index i from list l. Undefined behavior, if index does not exist. -
removeFromEnd(l,i)sig(l: list[T], i: numeric) => T. Remove the element at index length(l)-1-i from list l. Undefined behavior, if index does not exist. -
removeFirst(l)sig(l: list[T]) => void. Remove the first element from list l. Undefined behavior, if that does not exist. -
removeLast(l)sig(l: list[T]) => void. Remove the last element from list l. Undefined behavior, if that does not exist. -
replace(l,i,v)sig(l: list[T], i: numeric, v: T) => void. Replace the element at index i with val in list l. Undefined behavior, if index does not exist. -
replaceFromEnd(l,i,v)sig(l: list[T], i: numeric, v: T) => void. Replace the element at index length(l)-1-i with v in list l. Undefined behavior, if index does not exist. -
replaceFirst(l,v)sig(l: list[T], v: T) => void. Replace the first element in list l with v. Do nothing, if v is not found in the list. -
replaceLast(l,v)sig(l: list[T], v: T) => void. Replace the last element in list l with v. Undefined behavior, if index does not exist. -
insert(l,i,v)sig(l: list[T], i: numeric, v: T) => void. Insert v before the element at index i in list l. Undefined behavior, if index does not exist. -
insertFromEnd(l,i,v)sig(l: list[T], i: numeric, v: T) => void. Insert v before the element at index length(l)-1-idx in list l. Undefined behavior, if index does not exist. -
insertFirst(l,v)sig(l: list[T], v: T) => void. Insert v as the first element in list l. -
insertLast(l,v)sig(l: list[T], v: T) => void. Insert v as the last element in list l. -
subList(l,f,t)sig(l: list[T], f: numeric, t: numeric) => list[T]. Return the sublist from list l starting at index f until index t, both elements including. -
sum(l)sig(l: list[numeric]) => numeric. Sum of numeric values of list l. -
min(l)sig(l: list[numeric]) => numeric. Min of numeric values of list l. -
max(l)sig(l: list[numeric]) => numeric. Max of numeric values of list l. -
avg(l)sig(l: list[numeric]) => numeric. Average of numeric values of list l. -
median(l)sig(l: list[numeric]) => numeric. Median of numeric values of list l. -
stddev(l)sig(l: list[numeric]) => numeric. Standard deviation of numeric values of list l. -
random(l)sig(l: list[numeric]) => numeric. Value of a radomly selected item of the list l.
the group miscelleneous has the functions ...
-
append(s,t)sig(s: string, s: string) => void. Append the string t to the string s. Do not confuse with+, which returns a new string! -
v := esig(v: T, : T) => void. Assign the value of the expression e to the variable v.
An expression is, ...
- a constant,
- a variable,
- a function with a name defined in the section above (e.g.
get). Its parameters are expressions in turn.
Examples:
-
1+3 == round(3.6)is an expresion. -
pi+"4"is an expresion, even if it makes no sense as it is ill-typed (see below).
In the definition of statements below, expressions are used a lot as non terminals. They are written either <e>, or <f:expr> if
a "speaking" name f is needed in explanations.
if an expression is the following, ...
- a constant: implicitly it has the type as described in section "the list of types".
- a variable: variables must be declared before use. Its type is given in its declaration.
- a function: a function has a name (e.g.
get). The signature as defined for that name is retrieved and used (e.g. forgetthe signature is(l: list[T], i: numeric) => T) in the following way:- if the function has parameters (which are always expressions, e.g.
makelist(1,2,3)and1+1), the type of the parameter is derived following the rules as described here (e.g. formakelist(...)list[numeric]and for1+1numericis derived). - it is checked, whether the derived types match the parameter types. Type variables have to be instantiated consistently (e.g.
list[T]andlist[numeric]are unified, the result isTis instantiated tonumeric - if the derived types do not match, a type error is reported.
- if the derived types do match, the type of the function call is the result type in the signature(e.g. the result type is
T, this was instantiated tonumeric. Thusnumericis the result type of thegetcall).
- if the function has parameters (which are always expressions, e.g.
In NEPO`s simple type system, the type of a expression is never a type variable
Examples:
-
1+3 == 5is correctly typed and of typeboolean -
1+"4"is not correctly typed -
1 + 3is correctly typed and of typenumeric -
"1" + "3"is correctly typed and of typestring -
pi + e + round(3.6) > 6 && 1 == 1 || "1" == "1"is correctly typed and of typeboolean -
pi > "3"is not correctly typed
A BNF-style presentation is used. Non-terminals are surrounded by < >. Most terminals are left out to focus on the "pure" structure. See the important notes in the next
section "Concrete syntax".
<nepo-program> :=
<start-block> <func-decl>*
<start-block> :=
<var-decl>* <stmt>*
<func-with-result> :=
<name> <var-decl>* <concrete-type> <stmt>*
<func-without-result> :=
<name> <var-decl>* <stmt>*
<var-decl> :=
v t
Remark: Declare the variable with name v as from type t.
In version "2019" the name of the variable must be unique in the whole program.
In version "2020" this will change, when scopes are introduced.
Remark: t must be a concrete type. This are the green types from Fig.1, where T has to be replaced by a concrete type.
Thus numeric, list[numeric] and list[list[numeric]] are legal, list[T] is not legal.
<stmt> :=
<expr-statement>
| <if-stmt>
| <repeat-infinite>
| <repeat-while>
| <repeat-times>
| <repeat-iter>
| <repeat-foreach>
| <wait-until>
| <wait-sleep>
| <break>
| <continue>
| <return>
| <return-value>
<expr-statement> :=
<e>
Remark: The type of the expression must be void.
Otherwise a type error is reported.
<if-stmt> :=
<if-if-else>+ <else>?
<if-if-else> :=
<e> <stmt>*
Remark: The type of the expression must be boolean.
Otherwise a type error is reported.
<else> :=
<stmt>*
<repeat-infinite> :=
<stmt>*
<repeat-while> :=
<e> <stmt>*
Remark: The type of the expression must be boolean.
Otherwise a type error is reported.
<repeat-times> :=
<e> <stmt>*
Remark: The type of the expression must be numeric.
Otherwise a type error is reported.
<repeat-iter> :=
<var-decl> <f:expr> <u:expr> <i:expr> <stmt>*
Remark: the variable type and the types of the expressions f(rom) u(pper bound) and i(ncr) must be numeric.
Otherwise a type error is reported.
<repeat-foreach> :=
<var-decl> <e> <stmt>*
Remark: e must be of array type. The variable type and the element type of e must be the same.
Otherwise a type error is reported.
<wait-until> :=
(<e> <stmt>*)+
Remark: The type of the expression must be boolean.
Otherwise a type error is reported.
The sequence of expressions is evaluated until the first evaluating to true is found.
The corresponding statements are executed. The loop terminates afterwards.
If no expression evaluates to true, after a "short" sleeping time the evaluation is repeated.
<wait-sleep> :=
<e>
Remark: The type of the expression must be numeric.
Otherwise a type error is reported.
The value of the expression is the time to sleep.
<break> :=
# no data
Remark: only valid on the context of a <repeat-*>.
<continue> :=
# no data
Remark: only valid on the context of a <repeat-*>.
<return> :=
# no data
Remark: only valid on the context of a <func-without-result>.
<return-value> :=
<e>
Remark: only valid on the context of a <func-with-result>.
The type of e must match the return type of the function in which the statement is used.Nepo is designed in a way, that programs may have many different concrete syntaxes. Currently in the 2019 version we support a graphical notation, based on blockly. Blockly is an open-source framework (https://developers.google.com/blockly) used by many open-source projects for the graphical description of a program.
Thus if you point your browser to (https://lab.open-roberta.org/) and select a robot and then select the expert mode (to get access to all features), you will find for each of the syntactical elements as defined above (constants, variables, functions, BNF non-terminals) a matching blockly-block in the toolbox (please give us notice, if you believe that this is not true).
In the 2020 version of NEPO we will support in addition to the blockly-based notation textual notations, that will look like a subset of well-known programming languages: javascript, Java, C/C++ and python. Each of these language subset will 1:1 relate to the syntactical elements as defined above. It will use the syntax of the programming language and assume only the existence of a small runtime library (list implementation, etc; in the case, it is needed).
This will, for instance, allow to switch from a C/C++ NEPO program to either blockly or Java presentation without any information loss. But note, that this is only true for the NEPO-related subset of the language.
All robots share the core language, that was described in part 1. But each robots has capabilities, that extends the core language. For instance, a robot may be able to move. In this case motor commands for one or more motors are available. These adds new statements and new functions to the NEPO language. If the robot supports driving (i.e. uses two motors in a coordinated way to move forward or to turn), even more is added. Robots support sensors. This usually adds functions. Robot support actors. This usually adds statements. There is a lot of overlap in the features of robot system. To avoid redundancy in the description as much as possible, the extensions of the core language are documented in groups and later for each robot is defined which groups it supports.
... to be continued ...
Home | Community | Installation | Team 
Installation Tutorials
- Instructions to run a openroberta lab server using DOCKER
- Instructions to run the Open Roberta Lab Server natively on ubuntu ‐ not recommended
- Raspberry Pi 2/3/4 and the Open Roberta Lab
- EV3 and leJOS
- EV3 and ev3dev
- Creating the OR leJOS image
- Arduino Create Agent
- Mbed DAL: Generation and automation
Development
-
Workflows
-
Architecture
-
Blockly
-
Software engineering issues
-
Misc
-
Notes on robots
Textual Representation
Contribution
Discussions on future development