-
Notifications
You must be signed in to change notification settings - Fork 1.1k
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
1 changed file
with
88 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,88 @@ | ||
| # [0892. 三维形体的表面积](https://leetcode.cn/problems/surface-area-of-3d-shapes/) | ||
|
|
||
| - 标签:几何、数组、数学、矩阵 | ||
| - 难度:简单 | ||
|
|
||
| ## 题目链接 | ||
|
|
||
| - [0892. 三维形体的表面积 - 力扣](https://leetcode.cn/problems/surface-area-of-3d-shapes/) | ||
|
|
||
| ## 题目大意 | ||
|
|
||
| **描述**:给定一个 $n \times n$ 的网格 $grid$,上面放置着一些 $1 \times 1 \times 1$ 的正方体。每个值 $v = grid[i][j]$ 表示 $v$ 个正方体叠放在对应单元格 $(i, j)$ 上。 | ||
|
|
||
| 放置好正方体后,任何直接相邻的正方体都会互相粘在一起,形成一些不规则的三维形体。 | ||
|
|
||
| **要求**:返回最终这些形体的总面积。 | ||
|
|
||
| **说明**: | ||
|
|
||
| - 每个形体的底面也需要计入表面积中。 | ||
|
|
||
| **示例**: | ||
|
|
||
| - 示例 1: | ||
|
|
||
|  | ||
|
|
||
| ```python | ||
| 输入:grid = [[1,2],[3,4]] | ||
| 输出:34 | ||
| ``` | ||
|
|
||
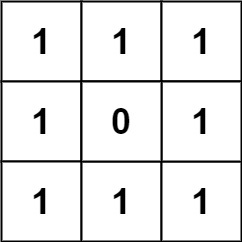
| - 示例 2: | ||
|
|
||
|  | ||
|
|
||
| ```python | ||
| 输入:grid = [[1,1,1],[1,0,1],[1,1,1]] | ||
| 输出:32 | ||
| ``` | ||
|
|
||
| ## 解题思路 | ||
|
|
||
| ### 思路 1:模拟 | ||
|
|
||
| 使用二重循环遍历所有的正方体,计算每一个正方体所贡献的表面积,将其累积起来即为答案。 | ||
|
|
||
| 而每一个正方体所贡献的表面积,可以通过枚举当前正方体前后左右相邻四个方向上的正方体的个数,从而通过判断计算得出。 | ||
|
|
||
| - 如果当前位置 $(row, col)$ 存在正方体,则正方体在上下位置上起码贡献了 $2$ 的表面积。 | ||
| - 如果当前位置 $(row, col)$ 的相邻位置 $(new\underline{}row, new\underline{}col)$ 上不存在正方体,说明当前正方体在该方向为最外侧,则 $(row, col)$ 位置所贡献的表面积为当前位置上的正方体个数,即 $grid[row][col]$。 | ||
| - 如果当前位置 $(row, col)$ 的相邻位置 $(new\underline{}row, new\underline{}col)$ 上存在正方体: | ||
| - 如果 $grid[row][col] > grid[new\underline{}row][new\underline{}col]$,说明 $grid[row][col]$ 在该方向上底面一部分被 $grid[new\underline{}row][new\underline{}col]$ 遮盖了,则 $(row, col)$ 位置所贡献的表面积为 $grid[row][col] - grid[new_row][new_col]$。 | ||
| - 如果 $grid[row][col] \le grid[new\underline{}row][new\underline{}col]$,说明 $grid[row][col]$ 在该方向上完全被 $grid[new\underline{}row][new\underline{}col]$ 遮盖了,则 $(row, col)$ 位置所贡献的表面积为 $0$。 | ||
|
|
||
| ### 思路 1:代码 | ||
|
|
||
| ```Python | ||
| class Solution: | ||
| def surfaceArea(self, grid: List[List[int]]) -> int: | ||
| directions = [(-1, 0), (0, 1), (1, 0), (0, -1)] | ||
| size = len(grid) | ||
|
|
||
| ans = 0 | ||
| for row in range(size): | ||
| for col in range(size): | ||
| if grid[row][col]: | ||
| # 底部、顶部贡献表面积 | ||
| ans += 2 | ||
| for direction in directions: | ||
| new_row = row + direction[0] | ||
| new_col = col + direction[1] | ||
| if 0 <= new_row < size and 0 <= new_col < size: | ||
| if grid[row][col] > grid[new_row][new_col]: | ||
| add = grid[row][col] - grid[new_row][new_col] | ||
| else: | ||
| add = 0 | ||
| else: | ||
| add = grid[row][col] | ||
| ans += add | ||
| return ans | ||
| ``` | ||
|
|
||
| ### 思路 1:复杂度分析 | ||
|
|
||
| - **时间复杂度**:$O(n^2)$,其中 $n$ 为二位数组 $grid$ 的行数或列数。 | ||
| - **空间复杂度**:$O(1)$。 | ||
|
|