-
Notifications
You must be signed in to change notification settings - Fork 1.2k
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
1. 二分查找知识内容优化 2. 更新目录章节链接
- Loading branch information
Showing
10 changed files
with
402 additions
and
314 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
148 changes: 148 additions & 0 deletions
148
Contents/01.Array/03.Array-Binary-Search/01.Array-Binary-Search-01.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,148 @@ | ||
| ## 1. 二分查找算法介绍 | ||
|
|
||
| ### 1.1 二分查找算法简介 | ||
|
|
||
| > **二分查找算法(Binary Search Algorithm)**:也叫做折半查找算法、对数查找算法,是一种用于在有序数组中查找特定元素的高效搜索算法。 | ||
| 二分查找的基本算法思想为:通过确定目标元素所在的区间范围,反复将查找范围减半,直到找到元素或找不到该元素为止。 | ||
|
|
||
| ### 1.2 二分查找算法步骤 | ||
|
|
||
| 以下是二分查找算法的基本步骤: | ||
|
|
||
| 1. **初始化**:首先,确定要查找的有序数据集合。可以是一个数组或列表,确保其中的元素按照升序或者降序排列。 | ||
| 2. **确定查找范围**:将整个有序数组集合的查找范围确定为整个数组范围区间,即左边界 $left$ 和右边界 $right$。 | ||
| 3. **计算中间元素**:根据 $mid = \lfloor (left + right) / 2 \rfloor$ 计算出中间元素下标位置 $mid$。 | ||
| 4. **比较中间元素**:将目标元素 $target$ 与中间元素 $nums[mid]$ 进行比较: | ||
| 1. 如果 $target == nums[mid]$,说明找到 $target$,因此返回中间元素的下标位置 $mid$。 | ||
| 2. 如果 $target < nums[mid]$,说明目标元素在左半部分($[left, mid - 1]$),更新右边界为中间元素的前一个位置,即 $right = mid - 1$。 | ||
| 3. 如果 $target > nums[mid]$,说明目标元素在右半部分($[mid + 1, right]$),更新左边界为中间元素的后一个位置,即 $left = mid + 1$。 | ||
|
|
||
| 5. 重复步骤 $3 \sim 4$,直到找到目标元素时返回中间元素下标位置,或者查找范围缩小为空(左边界大于右边界),表示目标元素不存在,此时返回 $-1$。 | ||
|
|
||
| 举个例子来说,以在有序数组 $[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]$ 中查找目标元素 $6$ 来说,使用二分查找算法的步骤如下: | ||
|
|
||
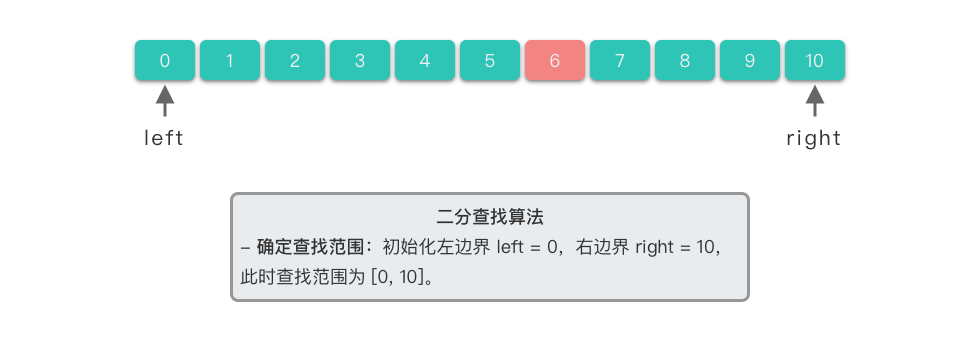
| 1. **确定查找范围**:初始时左边界 $left$ 为 $0$(数组的起始位置),$right$ 为 $10$(数组的末尾位置)。此时查找范围为 $[0, 10]$。 | ||
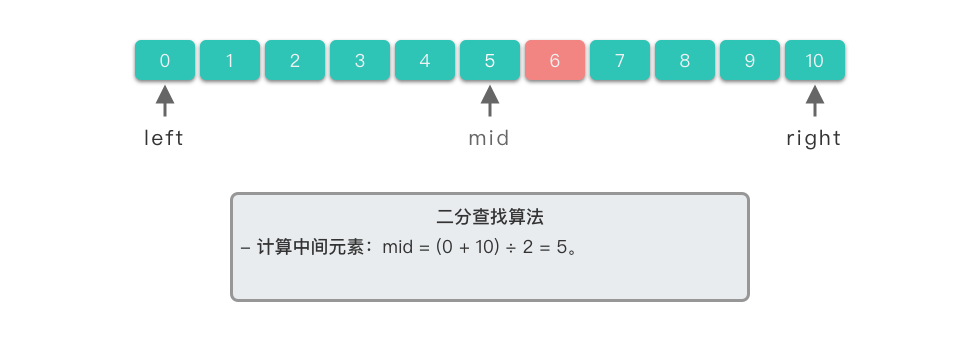
| 2. **计算中间元素**:中间元素下标位置为 $5$,对应元素为 $nums[5] == 5$。 | ||
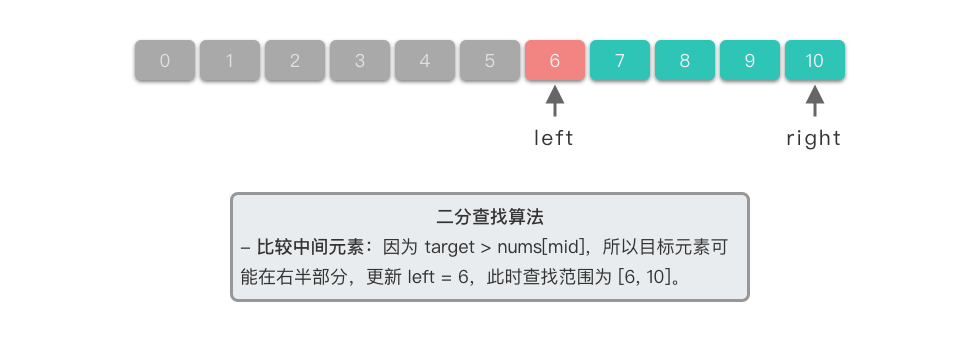
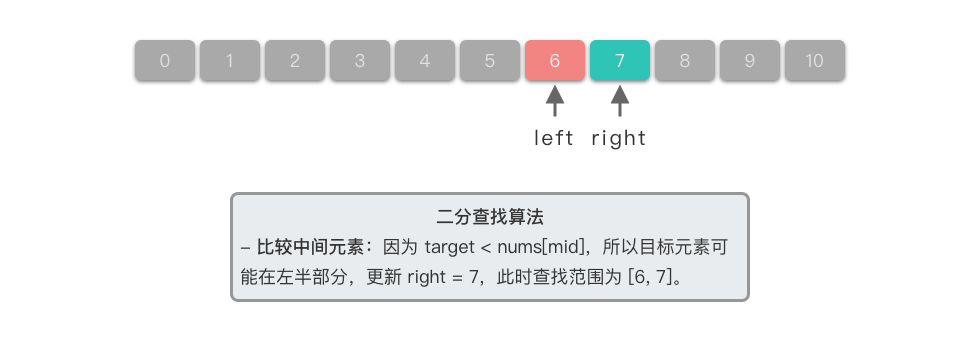
| 3. **比较中间元素**:因为 $6 > nums[5]$,所以目标元素可能在右半部分,更新左边界为中间元素的后一个位置,即 $left = 5$。此时查找范围为 $[5, 10]$。 | ||
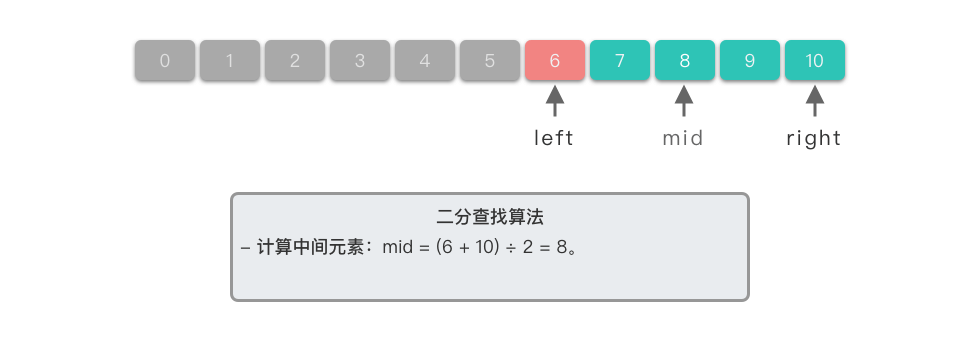
| 4. **计算中间元素**:中间元素下标位置为 $7$,对应元素为 $nums[7] == 7$。 | ||
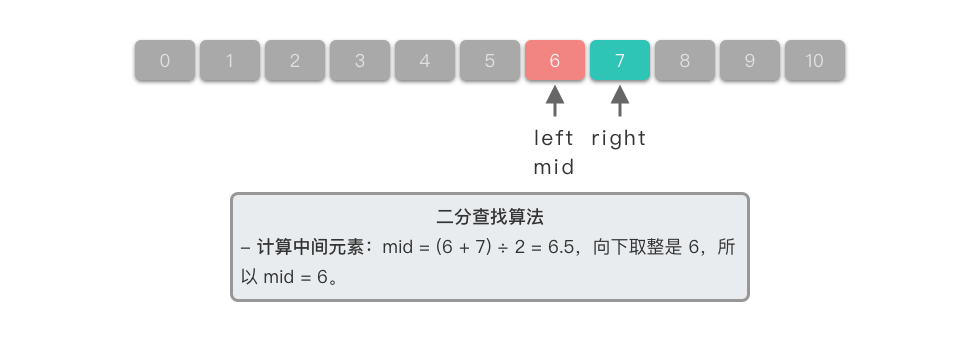
| 5. **比较中间元素**:因为 $6 < nums[7]$,所以目标元素可能在左半部分,更新右边界为中间元素的前一个位置,即 $right = 6$。此时查找范围为 $[5, 6]$。 | ||
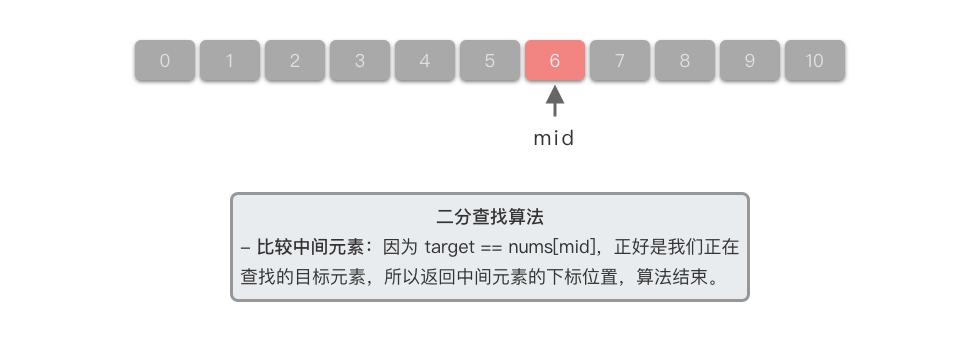
| 6. **计算中间元素**:中间元素下标位置为 $5$,对应元素为 $nums[5] == 5$。 | ||
| 7. **比较中间元素**:因为 $5 == nums[5]$,正好是我们正在查找的目标元素,此时返回中间元素的下标位置,算法结束。 | ||
|
|
||
| 于是我们发现,对于一个长度为 $10$ 的有序数组,我们只进行了 $3$ 次查找就找到了目标元素。而如果是按照顺序依次遍历数组,则在最坏情况下,我们可能需要查找 $10$ 次才能找到目标元素。 | ||
|
|
||
| ::: tabs#BinarySearch | ||
|
|
||
| @tab <1> | ||
|
|
||
|  | ||
|
|
||
| @tab <2> | ||
|
|
||
|  | ||
|
|
||
| @tab <3> | ||
|
|
||
|  | ||
|
|
||
| @tab <4> | ||
|
|
||
|  | ||
|
|
||
| @tab <5> | ||
|
|
||
|  | ||
|
|
||
| @tab <6> | ||
|
|
||
|  | ||
|
|
||
| @tab <7> | ||
|
|
||
|  | ||
|
|
||
| @tab <8> | ||
|
|
||
|  | ||
|
|
||
| ::: | ||
|
|
||
| ### 1.2 二分查找算法思想 | ||
|
|
||
| 二分查找算法是经典的 **「减而治之」** 的思想。 | ||
|
|
||
| 这里的 **「减」** 是减少问题规模的意思,**「治」** 是解决问题的意思。**「减」** 和 **「治」** 结合起来的意思就是 **「排除法解决问题」**。即:**每一次查找,排除掉一定不存在目标元素的区间,在剩下可能存在目标元素的区间中继续查找。** | ||
|
|
||
| 每一次通过一些条件判断,将待搜索的区间逐渐缩小,以达到「减少问题规模」的目的。而于问题的规模是有限的,经过有限次的查找,最终会查找到目标元素或者查找失败。 | ||
|
|
||
| ## 2. 简单二分查找 | ||
|
|
||
| 下面通过一个简单的例子来讲解下二分查找的思路和代码。 | ||
|
|
||
| - 题目链接:[704. 二分查找](https://leetcode.cn/problems/binary-search/) | ||
|
|
||
| ### 2.1 题目大意 | ||
|
|
||
| **描述**:给定一个升序的数组 $nums$,和一个目标值 $target$。 | ||
|
|
||
| **要求**:返回 $target$ 在数组中的位置,如果找不到,则返回 $-1$。 | ||
|
|
||
| **说明**: | ||
|
|
||
| - 你可以假设 $nums$ 中的所有元素是不重复的。 | ||
| - $n$ 将在 $[1, 10000]$ 之间。 | ||
| - $nums$ 的每个元素都将在 $[-9999, 9999]$之间。 | ||
|
|
||
| **示例**: | ||
|
|
||
| ```python | ||
| 输入: nums = [-1,0,3,5,9,12], target = 9 | ||
| 输出: 4 | ||
| 解释: 9 出现在 nums 中并且下标为 4 | ||
|
|
||
|
|
||
| 输入: nums = [-1,0,3,5,9,12], target = 2 | ||
| 输出: -1 | ||
| 解释: 2 不存在 nums 中因此返回 -1 | ||
| ``` | ||
|
|
||
| ### 2.2 解题思路 | ||
|
|
||
| #### 思路 1:二分查找 | ||
|
|
||
| 1. 设定左右边界为数组两端,即 $left = 0$,$right = len(nums) - 1$,代表待查找区间为 $[left, right]$(左闭右闭区间)。 | ||
| 2. 取两个节点中心位置 $mid$,先比较中心位置值 $nums[mid]$ 与目标值 $target$ 的大小。 | ||
| 1. 如果 $target == nums[mid]$,则返回中心位置。 | ||
| 2. 如果 $target > nums[mid]$,则将左节点设置为 $mid + 1$,然后继续在右区间 $[mid + 1, right]$ 搜索。 | ||
| 3. 如果 $target < nums[mid]$,则将右节点设置为 $mid - 1$,然后继续在左区间 $[left, mid - 1]$ 搜索。 | ||
| 3. 如果左边界大于右边界,查找范围缩小为空,说明目标元素不存在,此时返回 $-1$。 | ||
|
|
||
| #### 思路 1:代码 | ||
|
|
||
| ```python | ||
| class Solution: | ||
| def search(self, nums: List[int], target: int) -> int: | ||
| left, right = 0, len(nums) - 1 | ||
|
|
||
| # 在区间 [left, right] 内查找 target | ||
| while left <= right: | ||
| # 取区间中间节点 | ||
| mid = (left + right) // 2 | ||
| # 如果找到目标值,则直接返回中心位置 | ||
| if nums[mid] == target: | ||
| return mid | ||
| # 如果 nums[mid] 小于目标值,则在 [mid + 1, right] 中继续搜索 | ||
| elif nums[mid] < target: | ||
| left = mid + 1 | ||
| # 如果 nums[mid] 大于目标值,则在 [left, mid - 1] 中继续搜索 | ||
| else: | ||
| right = mid - 1 | ||
| # 未搜索到元素,返回 -1 | ||
| return -1 | ||
| ``` | ||
|
|
||
| #### 思路 1:复杂度分析 | ||
|
|
||
| - **时间复杂度**:$O(\log n)$。 | ||
| - **空间复杂度**:$O(1)$。 |
Oops, something went wrong.