This package contains utilities for solving sudoku puzzles using a variety of different algorithms.
The easiest way to install the package is to download it from PyPI using pip.
Note that sudoku depends on Python 3.7 or newer; please
ensure that you have a semi-recent version of Python installed before proceeding.
Run the following command in a shell (a UNIX-like environment is assumed):
$ pip install sudoku-ui
The package does not have any dependencies besides Python itself. If you wish to sandbox your installation inside a virtual environment, you may choose to use virtualenvwrapper or a similar utility to do so.
When successfully installed, a program called sudoku will be placed on your PATH. See the
Usage section below for details about how to use this program.
At any time, you can use the -h or --help flags to see a summary of options that the program accepts.
$ sudoku -h
usage: sudoku [-h] [-s SUDOKU] [-n NAME] [-a {brute-force,constraint,dlx}] [-g] [-d DELAY] [-q]
Solve sudoku puzzles.
optional arguments:
-h, --help show this help message and exit
-s SUDOKU, --sudoku SUDOKU, --string SUDOKU, --sudoku-string SUDOKU
A string representing a sudoku puzzle to solve
-n NAME, --name NAME The name of a sample puzzle to solve (for demo purposes)
-a {brute-force,constraint,dlx}, --algorithm {brute-force,constraint,dlx}
The algorithm to use to solve the puzzle
-g, --gui, --ui Display a GUI showing the puzzle being solved (not available for DLX mode)
-d DELAY, --delay DELAY, --delay-millis DELAY
How long to delay between steps in solving the puzzle (only applies in GUI mode)
-q, --quiet Reduce output verbosity (may be used multiple times)
The most basic usage is sudoku -s <string>, where <string> is a string representing a sudoku
puzzle to solve. The string should contain the value for each cell in the puzzle as a digit, or
a 0 or . for cells that are empty. Any other characters in the string will be ignored. For
example, the following three strings all represent the same puzzle to the program:
4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
400000805
030000000
000700000
020000060
000080400
000010000
000603070
500200000
104000000
4 . . |. . . |8 . 5
. 3 . |. . . |. . .
. . . |7 . . |. . .
------+------+------
. 2 . |. . . |. 6 .
. . . |. 8 . |4 . .
. . . |. 1 . |. . .
------+------+------
. . . |6 . 3 |. 7 .
5 . . |2 . . |. . .
1 . 4 |. . . |. . .
By default, sudoku will use its fastest algorithm to solve the puzzle. This is a
constraint-based algorithm which uses the rules of sudoku to quickly deduce the solution
to any input puzzle (assuming the puzzle has enough clues to be solved). The constraint-based
algorithm typically solves a sudoku in about 0.1 seconds (tested on a mid-2015 MacBook Pro).
The implementation of the constraint-based solution algorithm is based heavily on the prior work
of Peter Norvig.
To specify a different algorithm, use the -a or --algorithm flags to sudoku. The other
available algorithms are brute-force and dlx. A description of each of these algorithms follows.
The brute-force algorithm tries all possible values for all empty cells in the puzzle, and therefore its running time is exponential in the number of empty cells, i.e., O(9^n) where n is the number of empty cells. Given a sudoku puzzle designed specifically to thwart the brute-force strategy, this algorithm could take longer than the lifetime of the universe to find the solution! In practice, however, this algorithm typically takes about 10 minutes to solve even a fairly hard sudoku.
The DLX algorithm uses the "dancing links" algorithm (due to Don Knuth) to solve a sudoku puzzle by mapping it onto an equivalent exact cover problem and using a Python implementation of dancing links to solve the exact cover problem. This algorithm by far the slowest of the three, often taking over a day to solve a typical input puzzle. Profiling is needed to figure out where this algorithm is spending all of its time, since in theory this strategy should be at least as efficient (if not more efficient) than the brute-force approach. A re-implementation of the DLX algorithm in Go may be developed at some point in order to compare its performance against the (slow) Python implementation found here.
The sudoku.sample_puzzles module provides some sample sudoku puzzles for purposes of demoing or
testing the sudoku solver. The following puzzles are available:
- empty-n (1 ≤ n ≤ 64) - a sudoku puzzle with n empty cells (the remaining cells are already solved with the correct values); these are useful for functional and performance testing of the slower algorithms
- hard-n (1 ≤ n ≤ 95) - a hard sudoku puzzle with only the initial clue cells already solved
Instead of providing a sudoku string to solve when running the sudoku program, you may instead provide the name
of a sample puzzle to solve instead. To solve a sample puzzle, use the -n or --name flags to sudoku to specify
the puzzle name instead of using the -s or --sudoku flags. An example of this usage would be
sudoku -n hard-42 to solve the puzzle named hard-42. All other flags such as -a (see Algorithms above), -g
(see GUI Mode, below), and -q (see Output, below) are treated the same when using -n as when using -s.
For programmatic access to the sample puzzles, the get_puzzle_by_name function in the sample_puzzles module
accepts a string representing a puzzle name (see above) and returns a string representation of the corresponding
(unsolved) sudoku puzzle (see the Usage section above). For example:
>>> from sudoku.sample_puzzles import get_puzzle_by_name
>>> puzzle = get_puzzle_by_name('hard-57')
>>> puzzle
'1....786...7..8.1.8..2....9........24...1......9..5...6.8..........5.9.......93.4'When running in non-GUI mode (the default), the sudoku program prints output to the console before, during, and
after solving the given puzzle. Sample output from running the sudoku program on one of the included sample puzzles
(see Sample Puzzles, above) is as follows.
$ sudoku -n hard-25
Starting puzzle:
+-------+-------+-------+
| 1 . . | . . . | 7 . 9 |
| . 4 . | . . 7 | 2 . . |
| 8 . . | . . . | . . . |
+-------+-------+-------+
| . 7 . | . 1 . | . 6 . |
| 3 . . | . . . | . . 5 |
| . 6 . | . 4 . | . 2 . |
+-------+-------+-------+
| . . . | . . . | . . 8 |
| . . 5 | 3 . . | . 7 . |
| 7 . 2 | . . . | . 4 6 |
+-------+-------+-------+
Solving for 58 unknown cells using the constraint based algorithm...
Done! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.
+-------+-------+-------+
| 1 2 3 | 4 5 6 | 7 8 9 |
| 6 4 9 | 8 3 7 | 2 5 1 |
| 8 5 7 | 2 9 1 | 6 3 4 |
+-------+-------+-------+
| 2 7 4 | 5 1 8 | 9 6 3 |
| 3 9 8 | 6 7 2 | 4 1 5 |
| 5 6 1 | 9 4 3 | 8 2 7 |
+-------+-------+-------+
| 4 1 6 | 7 2 5 | 3 9 8 |
| 9 8 5 | 3 6 4 | 1 7 2 |
| 7 3 2 | 1 8 9 | 5 4 6 |
+-------+-------+-------+
123456789649837251857291634274518963398672415561943827416725398985364172732189546
Note that the real output will be colorized, with the initial clue cells of the puzzle colored cyan to differentiate them from the cells that were solved by the program. The program currently does not support disabling colorized output.
To reduce the verbosity of the output, the program accepts a flag called -q (--quiet). This flag may be
given up to three times, with less output being printed for each additional use of the flag.
The following is a sample of the output when running with the verbosity reduced by one level.
$ sudoku -n hard-25 -q
Solving for 58 unknown cells using the constraint based algorithm...
Done! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.
+-------+-------+-------+
| 1 2 3 | 4 5 6 | 7 8 9 |
| 6 4 9 | 8 3 7 | 2 5 1 |
| 8 5 7 | 2 9 1 | 6 3 4 |
+-------+-------+-------+
| 2 7 4 | 5 1 8 | 9 6 3 |
| 3 9 8 | 6 7 2 | 4 1 5 |
| 5 6 1 | 9 4 3 | 8 2 7 |
+-------+-------+-------+
| 4 1 6 | 7 2 5 | 3 9 8 |
| 9 8 5 | 3 6 4 | 1 7 2 |
| 7 3 2 | 1 8 9 | 5 4 6 |
+-------+-------+-------+
123456789649837251857291634274518963398672415561943827416725398985364172732189546
The following is a sample of the output when running with the verbosity reduced by two levels.
$ sudoku -n hard-25 -qq
Solving for 58 unknown cells using the constraint based algorithm...
Done! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.
123456789649837251857291634274518963398672415561943827416725398985364172732189546
The following is a sample of the output when running with the verbosity reduced by three levels (the maximum).
$ sudoku -n hard-25 -qqq
123456789649837251857291634274518963398672415561943827416725398985364172732189546
When running with minimal output, the program only prints the condensed version of the solved puzzle to the console.
This output is suitable for piping to other utilities for further processing. In this way, the sudoku program may
be used in a shell script, pipeline, or other non-interactive environment.
When running with more than minimal output (i.e., -q, -qq, or no -q flag at all), the program will print a .
character to the console for every 1,000 possibilities it tries while attempting to solve the puzzle. For the
constraint-based algorithm (the default), the puzzle is usually solved well in advance of 1,000 possibilities being
tried. For the brute-force and DLX algorithms, however, the . characters serve to show that the program is still
working, since otherwise there is no way to tell if the program is doing anything (except, perhaps, by measuring
the fan speed of the computer running the program).
When the program runs successfully, it exits with a code of zero (0). If the program encounters an error in parsing the arguments that were passed to it, it exits with a code of one (1). If the program fails to solve the given puzzle, it exits with a code of two (2).
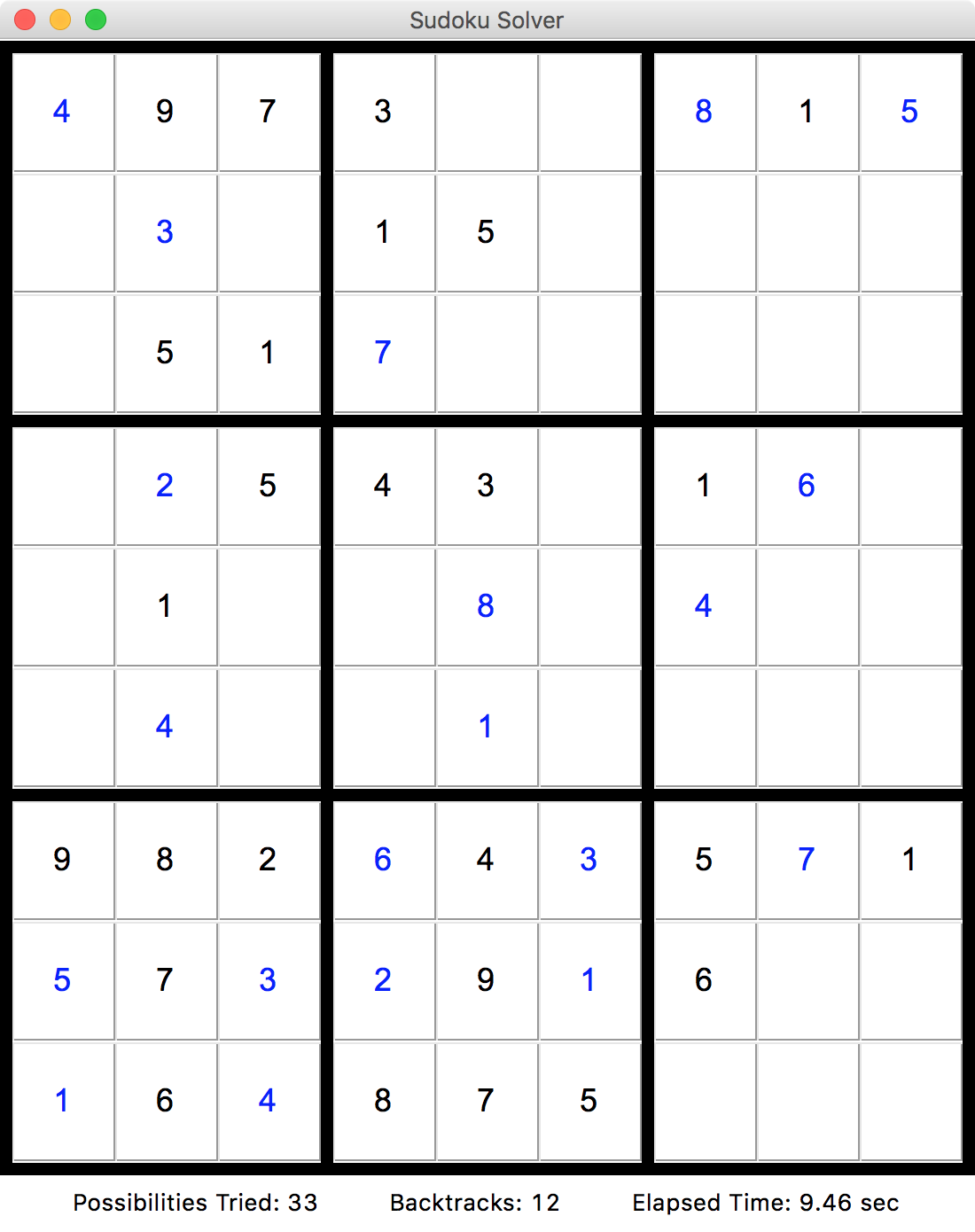
In order to help visualize the process of solving a given sudoku puzzle, the program also has a GUI mode, which can be
activated with the -g (--gui) flag to sudoku. When running in GUI mode, no output is printed to the console.
Instead, a window will open showing the sudoku puzzle being solved, with statistics along the bottom showing in real
time how many possibilities have been tried so far, how many times the algorithm has backtracked, and how much time
has elapsed since the solver began running.
By default, the puzzle will be solved as fast as possible, and the GUI will be updated very frequently as the solver
makes progress on solving the puzzle. However, this often means that the state of the puzzle is being updated so
quickly that it is impossible for an observer to keep up with the progress of the solver. In order to sidestep this
problem, the -d (--delay) flag to sudoku will delay updates to the GUI by the given number of milliseconds
at each step in the solution. For example, passing -d 500 will pause the GUI for half a second (500 milliseconds)
after each time the puzzle is changed. This makes it far easier to understand what is happening at each step in the
solving process. (Note that, even with no artificial delay, it will take slightly longer to solve a given puzzle in
GUI mode than it will to solve the same puzzle in non-GUI mode.)
Unfortunately, the DLX algorithm does not lend itself to being visualized with a constantly-updating sudoku puzzle. This is because the DLX algorithm transforms the problem of solving a sudoku into a different type of problem involving constraint sets and matrices, and the underlying relationship to a sudoku puzzle is obscured at best. For this reason, GUI mode is not available when using the DLX algorithm.
A sample of the program running in GUI mode is shown below.