Skip to content

Latest commit

 

History

History
432 lines (320 loc) · 16.7 KB

README_ch.MD

File metadata and controls

432 lines (320 loc) · 16.7 KB

布料模拟

Summary

传统的布料模拟使用的是基于力的做法，其基本步骤为：

  • 根据位置约束计算出质点受力
  • 根据受力计算出加速度
  • 利用加速度迭代速度
  • 利用速度迭代位置

但这种模拟方式需要较小的迭代步长，计算量较大，所以我使用了Position Base Dynamics算法，同时使用了unity的Job System进行并行计算，该算法的优点是可以使用较大的迭代步长，并且Job System配合Burst编译，性能非常可观。

PBD(Position Base Dynamics) Process

PBD算法的流程如下

图中x为当前质点位置,p为预测质点位置。可以看到:

  • 算法在每一帧开始时，会根据外力和阻尼先于计算一个位置(p)
  • 根据当前位置(x)和预测位置(p)，去进行碰撞检测，如果发现有碰撞，就生成一个碰撞约束
  • 迭代求解所有约束，最终会得到新预测位置p
  • 利用p - x 来计算速度v，并将p赋值给x
  • 最后再计算一遍速度(处理碰撞反弹之类速度变换)

外部力和约束的定义

像重力、风、可以视为外部力，但是像质点之间的相互作用我们通常视为内部约束，而非力。同样外部物体对质点的碰撞，也视为碰撞约束而不是外部力。

质点及布料模型

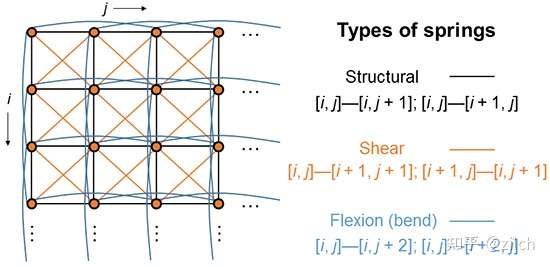
在物理上，我们通常可以将布料视作由一个个质点组成的结构。质点之间满足一定的约束条件，来模拟布料内部的作用力，如下图所示:

在传统的基于力的模拟中，质点之间的约束通常是用胡克定律以弹簧振子的形式去模拟。但是在基于位置的方案中，我们将会采用另外一种约束公式。

质点与布料模型顶点一一对应，然后让三角形的边作为顶点之间的约束。 好处是无需额外的骨骼绑定工作，我们可以针对满足一定的拓扑条件的任意Mesh进行布料模拟(1:一条边只被两个三角形共享 2:不封闭)，坏处是如果模型顶点较多，将比较耗费性能。

质量生成算法

通常来说，我们可以给一块布指定其密度(kg/m^2)。 这样的话，我们就可以根据Mesh的面积来计算质量。具体来说就是:

  • 遍历Mesh的所有三角面
  • 计算每个三角面的面积，乘以密度得到质量
  • 将质量三等份，分别累加给每个顶点
_masses = new NativeList<float>(this.vertexCount,Allocator.Persistent);
_masses.Resize(this.vertexCount,NativeArrayOptions.ClearMemory);
for(var i = 0; i < indices.Length / 3; i++){
    var offset = i * 3;
    var i0 = indices[offset];
    var i1 = indices[offset + 1];
    var i2 = indices[offset + 2];
    var v0 = vertices[i0];
    var v1 = vertices[i1];
    var v2 = vertices[i2];
    var area = IntersectUtil.GetArea(v0,v1,v2);
    var m = area * _setting.density;
    var m3 = m / 3;
    _masses[i0] += m3;
    _masses[i1] += m3;
    _masses[i2] += m3;
}

预测位置计算

为了使用JobSystem进行并行计算，我们可以实现一个如下的结构:

struct PositionEstimateJob : IJobParallelFor
{
    [ReadOnly] 
    public NativeArray<float3> positions;
    [ReadOnly] 
    public NativeArray<float3> velocities;
    [ReadOnly]
    public NativeArray<float3> normals;
    [ReadOnly]
    public NativeArray<float> masses;
    [WriteOnly]
    public NativeArray<float3> predictPositions;
    public float3 fieldForce;
    public float damper;
    public float dt;

    public void Execute(int index)
    {
      var p = positions[index];
      var v = velocities[index];
      var m = masses[index];
      //....
    }
}

JobSystem将会在多线程上并发执行Execute函数，在这里将会针对每个质点执行一次Execute函数，index为当前执行的任务索引(也即质点索引)。由于在这一步每个质点只更新自己的预测位置，不存在Race Condition，因此可以进行无锁并发。

在这里，我们输入的数据有:

  • positions - 位置
  • velocities - 速度
  • normals - 法线
  • masses - 质量
  • fieldForce - 外部场力,例如风力
  • damper - 阻尼系数 *dt - 迭代时间

输出为:

  • predictPositions

位置预测公式如下:

这三条公式，第一步为预测速度，第二步对速度施加阻尼，其中kd为阻尼系数，第三步利用速度预测位置。

g为重力加速度， Fe为作用于质点的外力，在本例里我们只用到了风力。 风对质点的作用力，需要投影到质点的法线方向，这也是为什么这个Job的输入需要有法线信息。

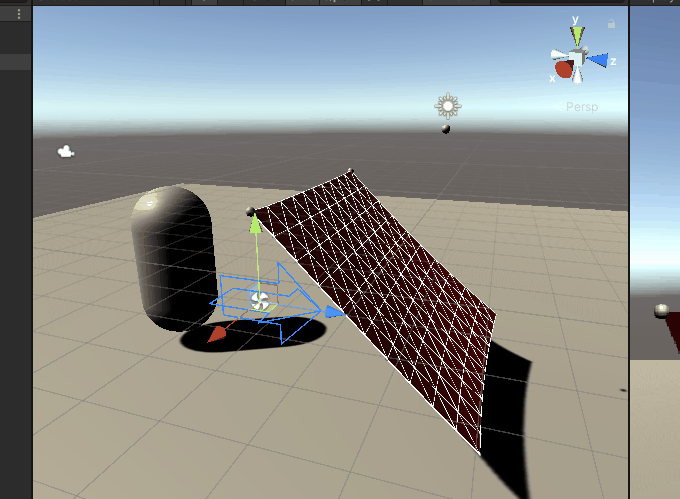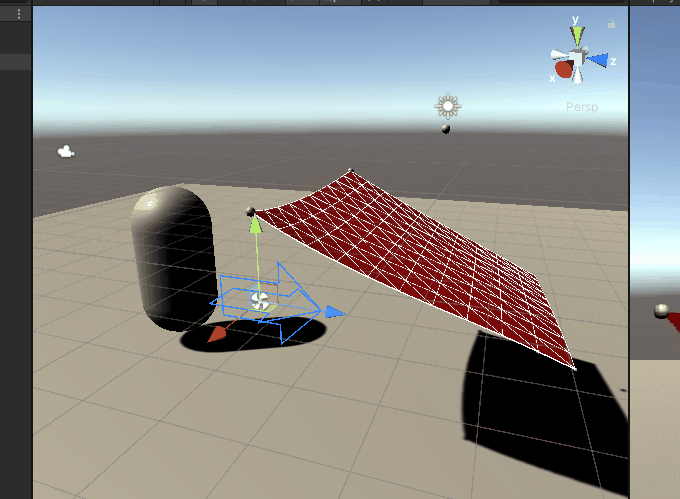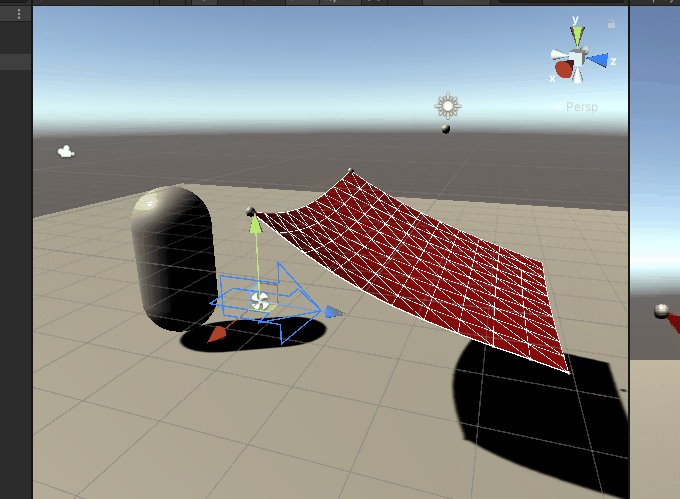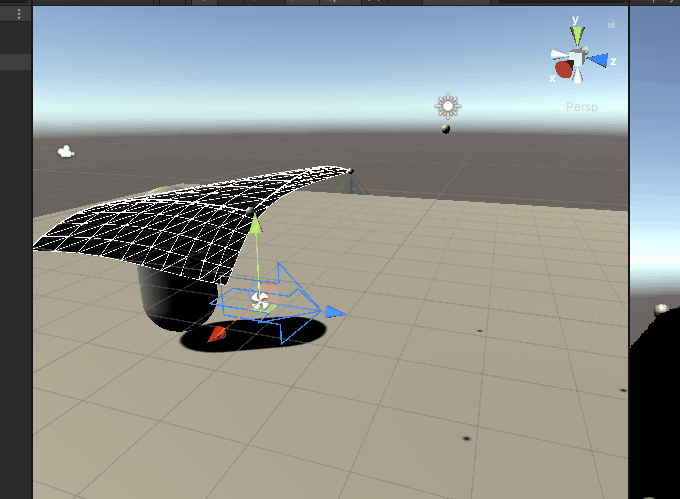
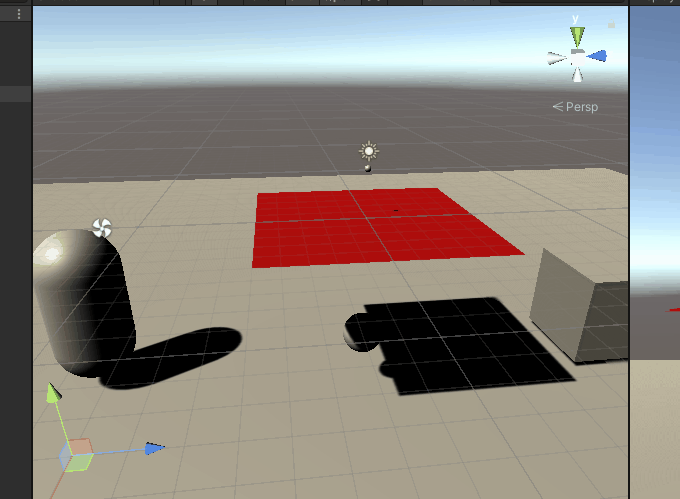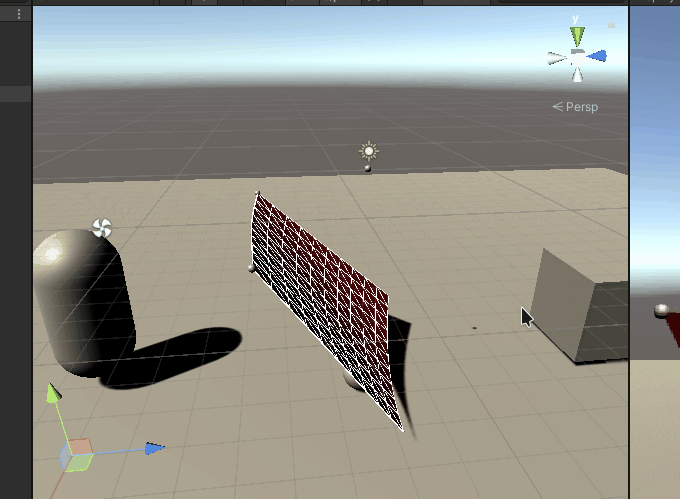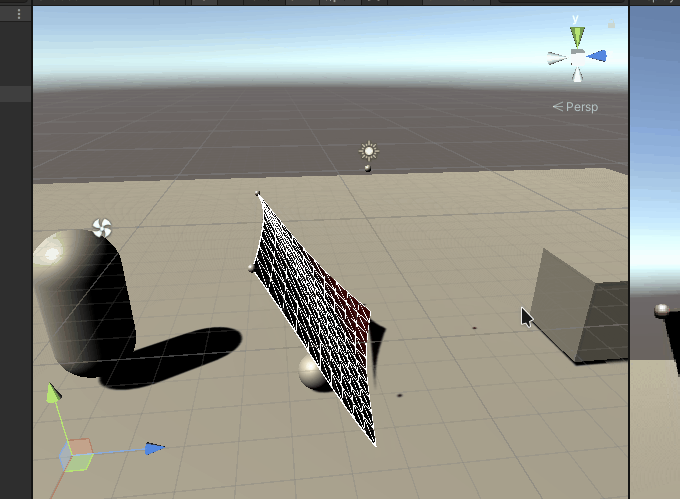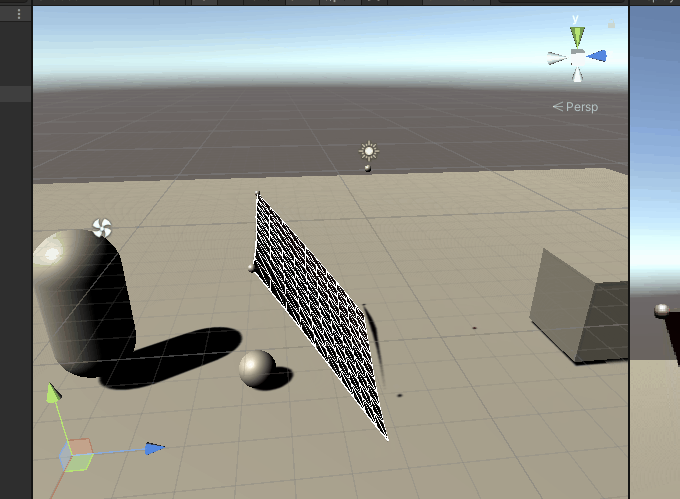
随风舞动的效果：

HbdOat.gif

Collisions

针对球体(Sphere)、方体(Box)、胶囊(Capsule)三种基础类型的碰撞检测。为简单起见，目前采用离散的检测方式，即判断质点是否在相关碰撞体内部。

算法流程为:

for position, predictPosition,index in vertices:
  for collider in colliders:
    concat = CheckCollision(position,predictPosition,collider)
    if concat:
      AddCollisionConstraint(index,concat.position,concat.normal)
  • 遍历所有质点，取其位置和预测位置，与所有的碰撞体做检测
  • 如果发现进入碰撞体内部，则计算出碰撞体表面距离当前质点最近的一个点
  • 对当前质点施加一个碰撞约束，让其在后面的约束迭代中强行离开碰撞体，回到表面去。

在IntersectUtil这个类里。我们实现了判定一个点是否在碰撞体内部

public static bool GetClosestSurfacePoint(float3 p, SphereDesc sphere, out ConcatInfo concatInfo)

GetClosestSurfacePoint它接收一个点p坐标，和一个碰撞体描述(SphereDesc)，如果发现点在碰撞体内部，就返回true,并且输出一个ConcatInfo结构。

ConcatInfo里保存了碰撞体表面距离p最近一个点的position和normal信息。

我们的目的是让这些碰撞体来约束布料的同时，布料也要反作用于这些碰撞体(假如是RigidBody的话)。

因此我们还需要额外定义一个刚体描述结构:

public struct RigidbodyDesc{
    public float mass;
    public float bounciness;
    public float3 velocity;
}

然后将RigidBody和Collider组合在一起:

public struct RigidbodyColliderDesc<T> where T:IColliderDesc{
    public int entityId;
    public T collider;
    public RigidbodyDesc rigidbody;
}

其中entityId后面会用来查找Unity对象。

然后定义个结构把所有需要与布料进行碰撞检测的数据整合在一起:

public struct CollidersGroup{
    private NativeList<RigidbodyColliderDesc<SphereDesc>> _spheres;
    private NativeList<RigidbodyColliderDesc<BoxDesc>> _boxes;
    private NativeList<RigidbodyColliderDesc<CapsuleDesc>> _capsules;
}

球体碰撞

public struct SphereDesc{
    public float3 center;
    public float radius;
}

胶囊碰撞

public struct CapsuleDesc{
    public float3 c0;
    public float4 axis; //xyz为单位化的方向，w为长度
    public float radius;
}

平行六面体

public struct BoxDesc{
    public float3 min;
    //3个边轴,xyz为normalzied的朝向，w为长度
    public float4 ax; 
    public float4 ay;
    public float4 az;
}

使用了xyz-min的角、和3个边向量来定义这个Box，严格来说，它能描述三维空间中的任意平行六面体。其中三个边向量，我们用float4保存，并且做了一些预计算。其xyz分量为单位向量，w分量向量长度。相关的预计算可以加速后面的碰撞检测。

Collision Job

我们需要用多线程任务并行执行碰撞检测和反作用力计算。

这个Job的输入输出数据结构

public struct CollisionJob : IJobParallelFor
{
    [ReadOnly]
    public float dt;
    [ReadOnly]
    public NativeArray<float3> positions;
    [ReadOnly]
    public NativeArray<float3> predictPositions;
    [ReadOnly]
    public NativeArray<float> masses;
    [ReadOnly]
    public CollidersGroup collidersGroup;
    [WriteOnly]
    public NativeArray<CollisionConstraintInfo> collisionConstraints;
    public NativeArray<ConstraintType> constraintTypes;
    public NativeList<RigidBodyForceApply>.ParallelWriter rigidBodyForceApplies;
}

它会根据当前质点的predictPosition和position信息，与CollidersGroup中的所有碰撞体进行碰撞检测，如果检测到有碰撞发生，则会做如下事情:

  • 修正predictPosition，避免碰撞发生
  • 将双方速度投影到接触点法线方向，利用动量守恒、动能公式重新计算双方在法线方向的速度
  • 将对Collider的速度修正贡献写入到rigidBodyForceApplies中，供后续实际作用到unity rigidboy对象。
  • 将对质点的约束信息写入到collisionConstraints中，供后续约束迭代阶段使用.

在法线方向上，碰撞引起的速度改变符合动量守恒定律

实际上，如果两个物体表面存在摩擦力，那么在垂直于法线的另一个方向上也会产生力的相互作用。但是在当前的这个版本里，我们暂且忽略了。

Constraints

在布料模拟中，存在如下几种约束:

  • 距离约束
  • 弯曲约束
  • 固定约束
  • 碰撞约束

距离约束

距离约束就是两个质点之间的距离，必须保持被约束在一定范围之内。

通常在布料初始化的时候，会记录下存在距离约束关系的质点之间的距离，称为RestLength。 在后续模拟中，当两个质点间距离小于RestLength时，我们就要将其推开，反之则要将他们拉拢。也即他们之间存在一根无形的弹簧。

两个质点之间的距离约束，要符合下述的迭代公式呢。为p1和p2分别计算出它们的修正量delta_p1和delta_p2。

原论文Matthias Müller, Position Based Dynamics, 2006 中给出了更一般的约束关系的公式推导，有兴趣可以看看，主要是用了牛顿-拉夫逊迭代法。

在本例中，我们根据三角面信息，为所有存在边连接的点建立距离约束。即:

private void BuildDistConstraints(){
    var edges = _meshModifier.edges;
    foreach(var e in edges){
        this.AddDistanceConstraint(e.vIndex0,e.vIndex1);
    }
}

距离约束结构定义:

public struct DistanceConstraintInfo{
    public float restLength;
    public int vIndex0;
    public int vIndex1;
}

弯曲约束

弯曲约束可以用来控制相邻两个面片的对折程度，这符合现实中布料的特性。 例如当我们将一块布料对折放置在平面上，其对折处会有一段弧形隆起。这就是布料内部结构存在的抵抗弯曲的力。 下图展示了一个弯曲约束的效果:

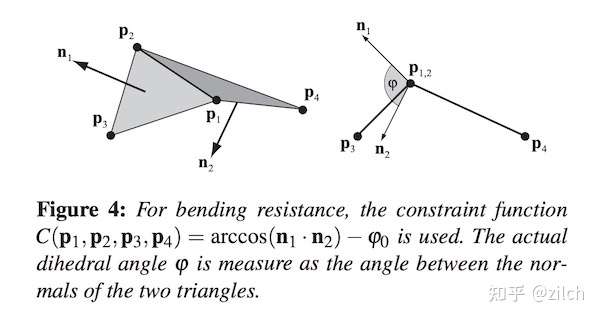
在布料建模中，弯曲约束可以由如下一幅图定义，来自上一节的论文:

两个相邻的三角面，共4个顶点，组成一个约束公式。

两个三角面的法线点乘，给出了三角面的夹角信息，在后续的模拟迭代中，我们只要约束这个夹角就行了。论文中同样给出了完整的计算公式推导过程:

弯曲约束的结构定义:

public struct BendConstraintInfo{
    public int vIndex0;
    public int vIndex1;
    public int vIndex2;
    public int vIndex3;
    public float rest; // angle
}

固定约束

这种约束是将某个质点固定在某个坐标上，令其无法移动。 所以这个约束的实现很简单，我们只要让这个质点位置不变，速度为0即可。

碰撞约束

我们之前提到了碰撞运算，但是在碰撞计算阶段并不会去直接修改质点的位置，而是生成一个碰撞约束，交由后续约束迭代阶段进行质点位置计算。

目前碰撞约束的结构很简单:

public struct CollisionConstraintInfo{
    public float3 concatPosition;
    public float3 normal;
    public float3 velocity;
}

在约束迭代阶段，质点会将自己的位置尽量往concatPosition去靠近。碰撞约束作为最高级约束，在其生效时，其他的约束不起作用。 velocity保存了碰撞计算得到的质点速度。

Iterations

约束迭代

考虑到Unity JobSystem的特性，目前实现的约束迭代流程如下:

  • Distance Constraint Job - 独立线程计算，把结果写入positionCorrect数组
  • Bend Constraint Job - 独立线程计算，依赖第一步完成，同样把结果累加到positionCorrect数组
  • Final Constraint Job - 多线程并发计算，会处理固定约束、碰撞约束，并且合并1,2两步生成的positionCorrect.
private JobHandle StartConstraintsSolveJob(JobHandle depend){
   JobHandle jobHandle = depend;
   var predictPositions = this._predictPositions;
   for(var i = 0; i < this.constraintSolverIteratorCount; i ++){
       jobHandle = StartDistanceConstraintsJob(jobHandle,i);
       jobHandle = StartBendConstraintsJob(jobHandle,i);
       jobHandle = StartFinalConstraintsJob(jobHandle,i);
   }
   return jobHandle;
}

更新质点位置和速度

在完成约束迭代计算之后，我们得到了一份最终版本的predictPositions。

然后利用以下公式完成速度和位置的更新:

velocity = (predictPosition - position)/dt
position = predictPosition

如果质点在之前的碰撞计算中得到了新的速度，那么这里采用碰撞计算的速度作为最新速度

public void Execute(int index)
{
   if( (constraintTypes[index] & ConstraintType.Collision) == ConstraintType.Collision){
       velocities[index] = this.collisionConstraintInfos[index].velocity;
   }else{
       velocities[index] = (predictPositions[index] - positions[index])/dt;
   }
   positions[index] = predictPositions[index];
}

这里同样是一个多线程并发计算的Job。

布料对外部物体施加力

在先前的CollisionJob阶段，我们已经完成了碰撞反馈计算，并把对场景Rigidbody的作用速度写入到了NativeList<RigidBodyForceApply>数组中。

那么接下来，我们只要取得这个数组，查找到对应的Rigidbody，对其使用AddForce()即可:

private void ApplyPhysicalSimulationToRigidbodies(){
   for(var i = 0; i < _rigidBodyForceApplys.Length; i ++){
       var forceInfo =  _rigidBodyForceApplys[i];
       _colliderProxies[forceInfo.entityId].attachedRigidbody.AddForce(forceInfo.velocity,ForceMode.VelocityChange);
   }
}

以下是布料下落推动一个球体向前滚动的效果:

Todo

连续碰撞检测

在离散碰撞检测下，我们只要检测质点是否位于碰撞体内部即可，但离散检测在速度较快、或者卡顿导致两帧之间物体位移较大的情况下会发生穿透现象。

连续性碰撞检测的出现就是为了修正这个问题。例如对于质点，我们可以将其前后两帧的位置连成一根线，然后判断这根线是否与碰撞体相交。很明显连续性碰撞检测需要的计算量是远大于离散性检测的，手写所有Collider的连续碰撞检测工作量较大，所以并未实现。

布料破坏

布料破坏的原理是比较简单的。即当两个质点之间的距离超出一定阈值，那么视为被撕裂，我们就移除这两个质点之间的距离约束。

但问题在于，我们需要动态去调整Mesh的拓扑结构。当布料被撕裂时，我们需要:

  • 在Mesh撕裂位置新增顶点
  • 调整附近三角面的顶点索引，插入新增的顶点，以起到让两个三角面分离的效果
  • 更新布料的距离约束、弯曲约束关系

以上需要我们在一开始的时候建立好布料的拓扑关系，以快速的根据顶点查询边、三角面等信息。 另一方面，如果存在动态增删布料顶点和相关约束关系的话，对数据结构的设计也是一种考验。

自相交

Liquid

todo