Cloth Simulation

Summary

Traditional cloth simulation uses a force-based approach, the basic steps of which are:

• Calculate the force of the particle according to the position constraint
• Calculate the acceleration according to the force
• Utilize acceleration to iterate speed
• Iterate position using velocity

However, this simulation method requires a small iterative step size and requires a large amount of calculation, so I used the Position Base Dynamics algorithm, and at the same time used Unity's Job System for parallel computing. The advantage of this algorithm is that it can use a larger iteration step. Long, and the Job System is compiled with Burst, the performance is very impressive.

PBD(Position Base Dynamics) Process

The flow of the PBD algorithm is as follows

In the figure, x is the current particle position, and p is the predicted particle position. can be seen:

• At the beginning of each frame, the algorithm calculates a position (p) before calculating the external force and damping
• According to the current position (x) and the predicted position (p), perform collision detection. If a collision is found, a collision constraint is generated
• Iteratively solve all constraints, and finally get a new predicted position p
• Calculate velocity v using p - x and assign p to x
• Finally calculate the speed again (processing speed transformation such as collision bounce)

Definition of External Forces and Restraints

Things like gravity and wind can be viewed as external forces, but interactions like particles are usually viewed as internal constraints rather than forces. Similarly, the collision of an external object against a particle is also regarded as a collision constraint rather than an external force.

Particle and cloth models

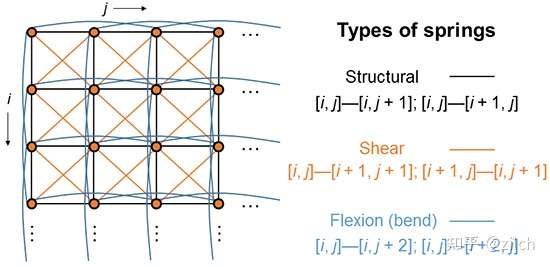
Physically, we can usually think of cloth as a structure composed of individual particles. The particles satisfy certain constraints to simulate the force inside the cloth, as shown in the following figure:

In traditional force-based simulations, the constraints between particles are usually modeled in the form of spring oscillators using Hooke's law. But in the location-based scheme, we will use another constraint formulation.

The mass points correspond to the vertices of the cloth model one-to-one, and then let the edges of the triangles act as constraints between the vertices. The advantage is that there is no need for additional bone binding work, we can perform cloth simulation for any Mesh that meets certain topology conditions (1: one edge is only shared by two triangles 2: not closed), the disadvantage is that if the model has many vertices, it will be Relatively expensive.

Mass Generation Algorithm

Generally speaking, we can assign a density (kg/m^2) to a piece of cloth. In this way, we can calculate the mass based on the area of the Mesh. Specifically:

• Traverse all triangle faces of Mesh
• Calculate the area of each triangular face, multiply by the density to get the mass
• Divide the mass into three equal parts and add them to each vertex separately

_masses = new NativeList<float>(this.vertexCount,Allocator.Persistent);
_masses.Resize(this.vertexCount,NativeArrayOptions.ClearMemory);
for(var i = 0; i < indices.Length / 3; i++){
    var offset = i * 3;
    var i0 = indices[offset];
    var i1 = indices[offset + 1];
    var i2 = indices[offset + 2];
    var v0 = vertices[i0];
    var v1 = vertices[i1];
    var v2 = vertices[i2];
    var area = IntersectUtil.GetArea(v0,v1,v2);
    var m = area * _setting.density;
    var m3 = m / 3;
    _masses[i0] += m3;
    _masses[i1] += m3;
    _masses[i2] += m3;
}

Predicted position calculation

In order to use JobSystem for parallel computing, we can implement a structure as follows:

struct PositionEstimateJob : IJobParallelFor
{
    [ReadOnly] 
    public NativeArray<float3> positions;
    [ReadOnly] 
    public NativeArray<float3> velocities;
    [ReadOnly]
    public NativeArray<float3> normals;
    [ReadOnly]
    public NativeArray<float> masses;
    [WriteOnly]
    public NativeArray<float3> predictPositions;
    public float3 fieldForce;
    public float damper;
    public float dt;

    public void Execute(int index)
    {
      var p = positions[index];
      var v = velocities[index];
      var m = masses[index];
      //....
    }
}

JobSystem will execute the Execute function concurrently on multiple threads. Here, the Execute function will be executed once for each particle, and index is the index of the currently executing task (ie, the particle index). Since each particle only updates its own predicted position in this step, there is no Race Condition, so lock-free concurrency can be performed.

Here, our input data are:

• positions - positions
• velocities - speed
• normals - normals
• masses - mass
• fieldForce - external field force, such as wind
• damper - damping coefficient *dt - iteration time

The output is:

• predictPositions

The location prediction formula is as follows:

In these three formulas, the first step is to predict the speed, the second step is to apply damping to the speed, where kd is the damping coefficient, and the third step uses the speed to predict the position.

g is the acceleration of gravity, Fe is the external force acting on the particle, in this example we only use the wind force. The force of the wind on the particle needs to be projected to the normal direction of the particle, which is why the input of this Job needs to have normal information.

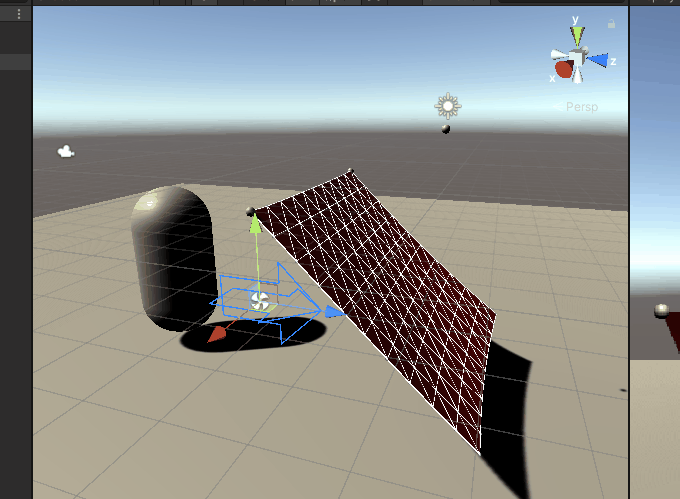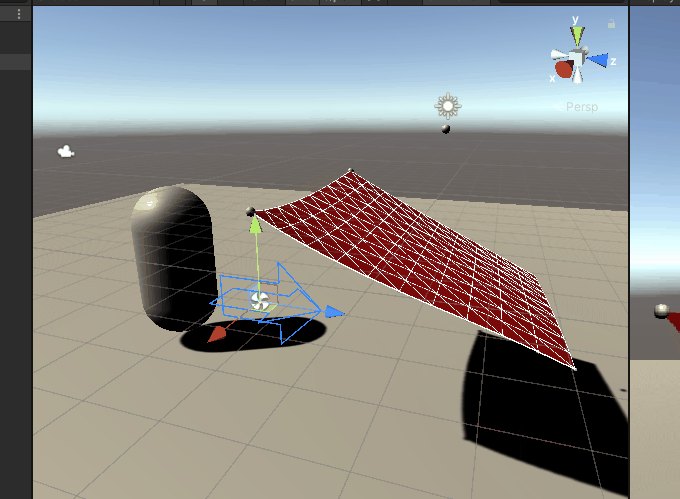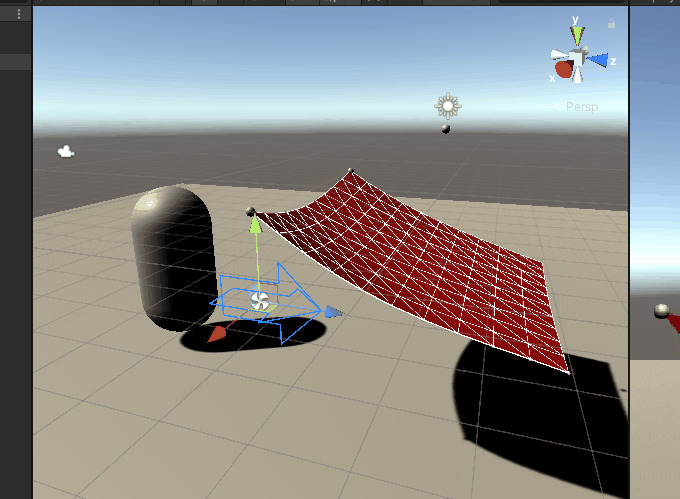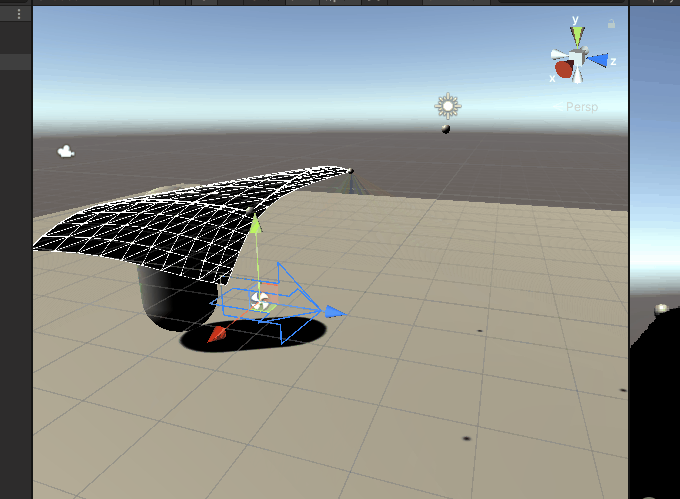
The effect of dancing with the wind:

Collisions

Collision detection for three basic types of Sphere, Box, and Capsule. For the sake of simplicity, a discrete detection method is currently used, that is, it is judged whether the particle is inside the relevant collision body.

The algorithm flow is:

for position, predictPosition,index in vertices:
  for collider in colliders:
    concat = CheckCollision(position,predictPosition,collider)
    if concat:
      AddCollisionConstraint(index,concat.position,concat.normal)

• Traverse all the particles, take their positions and predicted positions, and check with all the colliders
• If it is found to be inside the collider, calculate the closest point on the surface of the collider to the current particle
• Apply a collision constraint to the current particle, forcing it to leave the collider and return to the surface in subsequent iterations of the constraint.

In the IntersectUtil class. We implemented to determine whether a point is inside the collider

public static bool GetClosestSurfacePoint(float3 p, SphereDesc sphere, out ConcatInfo concatInfo)

GetClosestSurfacePoint It receives a point p coordinate, and a collision body description (SphereDesc), if the point is found inside the collision body, it returns true, and outputs a ConcatInfo structure.

ConcatInfo stores the position and normal information of the point closest to p on the surface of the collider.

Our goal is for these colliders to constrain the cloth, and at the same time the cloth also reacts to these colliders (if it is a RigidBody).

Therefore, we also need to define an additional rigid body description structure:

public struct RigidbodyDesc{
    public float mass;
    public float bounciness;
    public float3 velocity;
}

Then combine RigidBody and Collider together:

public struct RigidbodyColliderDesc<T> where T:IColliderDesc{
    public int entityId;
    public T collider;
    public RigidbodyDesc rigidbody;
}

The entityId will be used later to find the Unity object.

Then define a structure to integrate all the data needed for collision detection with the cloth:

public struct CollidersGroup{
    private NativeList<RigidbodyColliderDesc<SphereDesc>> _spheres;
    private NativeList<RigidbodyColliderDesc<BoxDesc>> _boxes;
    private NativeList<RigidbodyColliderDesc<CapsuleDesc>> _capsules;
}

Sphere collision

public struct SphereDesc{
    public float3 center;
    public float radius;
}

Capsule collision

public struct CapsuleDesc{
    public float3 c0;
    public float4 axis; //xyz为单位化的方向，w为长度
    public float radius;
}

Parallelepiped

public struct BoxDesc{
    public float3 min;
    //3个边轴,xyz为normalzied的朝向，w为长度
    public float4 ax; 
    public float4 ay;
    public float4 az;
}

The xyz-min angle and 3 edge vectors are used to define this Box. Strictly speaking, it can describe any parallelepiped in three-dimensional space. Three of the edge vectors, we save with float4, and do some precomputing. Its xyz components are unit vectors, and the w component vector length. The associated pre-computation can speed up later collision detection.

Collision Job

We need to perform collision detection and reaction force calculations in parallel with multithreaded tasks.

The input and output data structure of this Job

public struct CollisionJob : IJobParallelFor
{
    [ReadOnly]
    public float dt;
    [ReadOnly]
    public NativeArray<float3> positions;
    [ReadOnly]
    public NativeArray<float3> predictPositions;
    [ReadOnly]
    public NativeArray<float> masses;
    [ReadOnly]
    public CollidersGroup collidersGroup;
    [WriteOnly]
    public NativeArray<CollisionConstraintInfo> collisionConstraints;
    public NativeArray<ConstraintType> constraintTypes;
    public NativeList<RigidBodyForceApply>.ParallelWriter rigidBodyForceApplies;
}

It will perform collision detection with all colliders in the CollidersGroup based on the predictPosition and position information of the current particle. If a collision is detected, it will do the following:

• Fix predictPosition to avoid collision
• Project the speed of both parties to the normal direction of the contact point, and use the momentum conservation and kinetic energy formula to recalculate the speed of both parties in the normal direction
• Write the speed correction contribution to Collider into rigidBodyForceApplies for subsequent actual effects on the unity rigidboy object.
• Write the constraint information on the particle into collisionConstraints for use in subsequent constraint iteration stages.

In the normal direction, the velocity change caused by the collision follows the law of conservation of momentum

In fact, if there is friction between the surfaces of two objects, there will also be a force interaction in the other direction perpendicular to the normal. But in the current version, we ignore it for now.

Constraints

In cloth simulation, the following constraints exist:

• Distance constraints
• Bending constraints
• Fixed constraints
• Collision constraints

Distance constraints

A distance constraint is the distance between two particles, which must remain constrained within a certain range.

Usually when the cloth is initialized, the distance between the particles with the distance constraint relationship is recorded, which is called RestLength. In subsequent simulations, when the distance between the two particles is less than RestLength, we will push them apart, otherwise we will pull them together. That is, there is an invisible spring between them.

The distance constraint between two mass points must conform to the following iterative formula. Calculate their corrections delta_p1 and delta_p2 for p1 and p2, respectively.

The original paper Matthias Müller, Position Based Dynamics, 2006 gives a more general formula derivation of the constraint relationship, if you are interested, you can read it See, mainly using the Newton-Raphson iteration method.

In this example, we establish distance constraints for all points connected by edges based on the triangular face information. which is:

private void BuildDistConstraints(){
    var edges = _meshModifier.edges;
    foreach(var e in edges){
        this.AddDistanceConstraint(e.vIndex0,e.vIndex1);
    }
}

Definition of distance constraint structure:

public struct DistanceConstraintInfo{
    public float restLength;
    public int vIndex0;
    public int vIndex1;
}

Bending Constraints

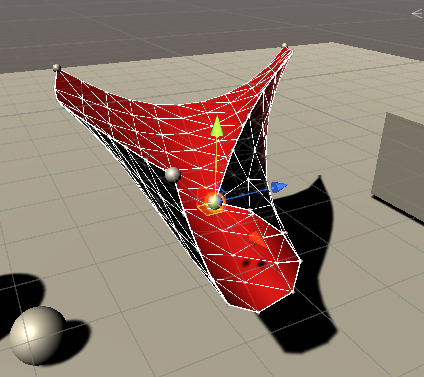
Bend constraints can be used to control the degree of folding between two adjacent patches, which is in line with the characteristics of real cloth. For example, when we fold a piece of fabric on a flat surface, there will be an arc-shaped bulge at the fold. This is the resistance to bending that exists in the inner structure of the cloth. The following image shows the effect of a bend constraint:

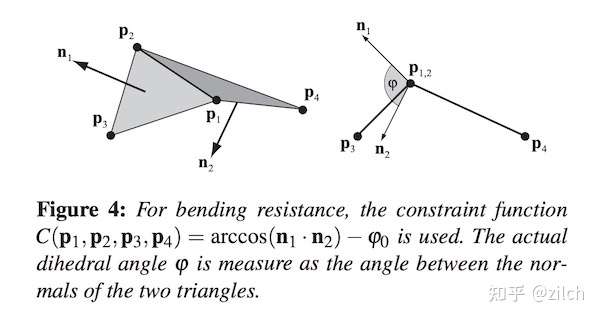
In cloth modeling, bending constraints can be defined by the following diagram, from the paper in the previous section:

Two adjacent triangular faces, with a total of 4 vertices, form a constraint formula.

The dot product of the normals of the two triangular faces gives the angle information of the triangular faces. In subsequent simulation iterations, we only need to constrain this angle. The paper also gives the complete calculation formula derivation process:

Structural Definition of Bending Constraints:

public struct BendConstraintInfo{
    public int vIndex0;
    public int vIndex1;
    public int vIndex2;
    public int vIndex3;
    public float rest; // angle
}

Fixed constraints

This constraint is to fix a particle at a certain coordinate so that it cannot move. So the implementation of this constraint is very simple, we only need to keep the position of the particle unchanged and the velocity to be 0.

Collision constraints

We mentioned the collision operation before, but in the collision calculation stage, the position of the particle is not directly modified, but a collision constraint is generated, and the particle position is calculated in the subsequent constraint iteration stage.

The structure of the current collision constraint is simple:

public struct CollisionConstraintInfo{
    public float3 concatPosition;
    public float3 normal;
    public float3 velocity;
}

In the constraint iteration phase, the particle will try to move as close to the concatPosition as possible. Collision constraints are the top-level constraints, and when they are in effect, other constraints have no effect. velocity holds the particle velocity calculated from the collision.

Iterations

Constrained iteration

Considering the characteristics of Unity JobSystem, the currently implemented constraint iteration process is as follows:

• Distance Constraint Job - independent thread calculation, write the result to the positionCorrect array
• Bend Constraint Job - independent thread calculation, relying on the first step to complete, also accumulate the results to the positionCorrect array
• Final Constraint Job - Multi-threaded concurrent calculation, it will process fixed constraints, collision constraints, and merge the positionCorrect generated by 1 and 2 steps.

private JobHandle StartConstraintsSolveJob(JobHandle depend){
   JobHandle jobHandle = depend;
   var predictPositions = this._predictPositions;
   for(var i = 0; i < this.constraintSolverIteratorCount; i ++){
       jobHandle = StartDistanceConstraintsJob(jobHandle,i);
       jobHandle = StartBendConstraintsJob(jobHandle,i);
       jobHandle = StartFinalConstraintsJob(jobHandle,i);
   }
   return jobHandle;
}

Update particle position and velocity

After iterative computation of constraints, we get a final version of predictPositions.

The velocity and position updates are then accomplished using the following formulas:

velocity = (predictPosition - position)/dt
position = predictPosition

If the particle has a new velocity in the previous collision calculation, then the collision calculation velocity is used as the latest velocity here

public void Execute(int index)
{
   if( (constraintTypes[index] & ConstraintType.Collision) == ConstraintType.Collision){
       velocities[index] = this.collisionConstraintInfos[index].velocity;
   }else{
       velocities[index] = (predictPositions[index] - positions[index])/dt;
   }
   positions[index] = predictPositions[index];
}

Here is also a multi-threaded concurrent computing Job.

Cloth exerts force on external objects

In the previous CollisionJob stage, we have completed the collision feedback calculation and written the action speed to the scene Rigidbody into the NativeList<RigidBodyForceApply> array.

Next, we just need to get this array, find the corresponding Rigidbody, and use AddForce() on it:

private void ApplyPhysicalSimulationToRigidbodies(){
   for(var i = 0; i < _rigidBodyForceApplys.Length; i ++){
       var forceInfo =  _rigidBodyForceApplys[i];
       _colliderProxies[forceInfo.entityId].attachedRigidbody.AddForce(forceInfo.velocity,ForceMode.VelocityChange);
   }
}

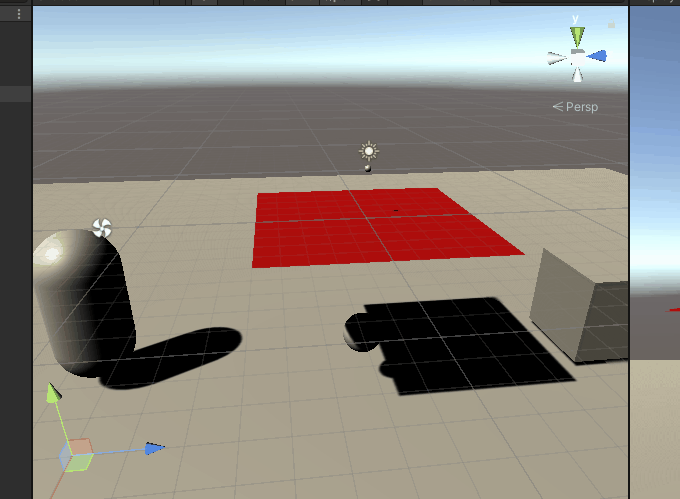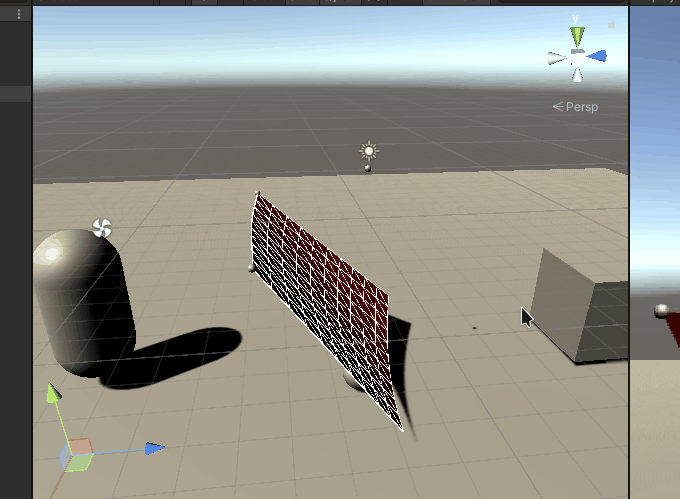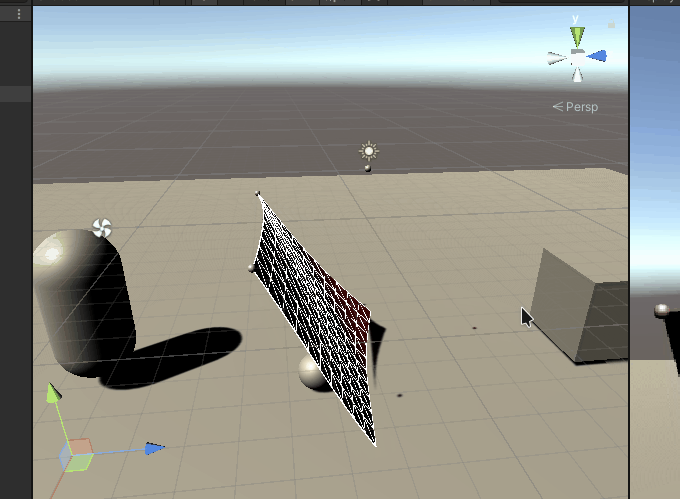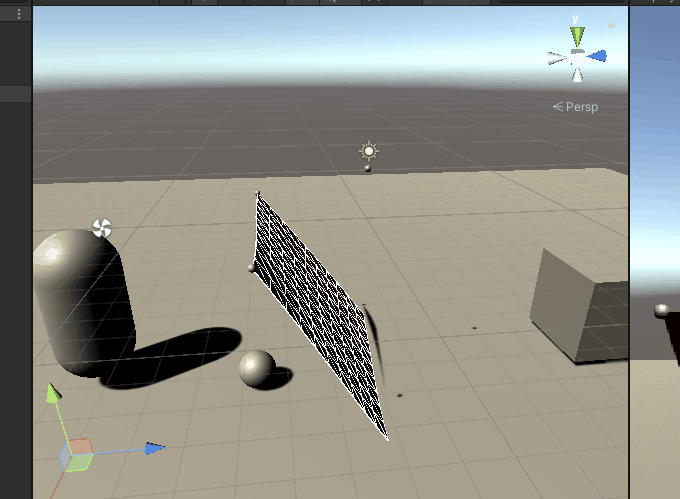
Here's the effect of falling cloth pushing a sphere forward:

Todo

Continuous collision detection

Under discrete collision detection, we only need to detect whether the particle is located inside the collision body, but the discrete detection will penetrate when the speed is fast, or when the object is stuttered and the displacement between the two frames is large.

Continuity collision detection came into existence to correct this problem. For example, for a mass point, we can connect the positions of the two frames before and after it into a line, and then determine whether this line intersects the collider. Obviously, the amount of computation required for continuous collision detection is much larger than discrete detection. The continuous collision detection of all Colliders by handwriting has a large workload, so it has not been implemented.

Cloth destruction

The principle of cloth destruction is relatively simple. That is, when the distance between the two particles exceeds a certain threshold, it is considered to be torn, and we remove the distance constraint between the two particles.

But the problem is that we need to dynamically adjust the topology of the Mesh. When the fabric is torn, we need to:

• Added vertices at the Mesh tearing position
• Adjust the vertex index of the nearby triangular face, insert the new vertex, to have the effect of separating the two triangular faces
• Update the distance constraints and bending constraints of the cloth

The above requires us to establish the topological relationship of the cloth at the beginning, so as to quickly query the information such as edges and triangles according to the vertices. On the other hand, if there are dynamic addition and deletion of cloth vertices and related constraints, the design of the data structure is also a test.

Self-intersection

Liquid

todo