python
Graphite can be scripted in Python, in two different ways (either Python in Graphite or
Graphite in Python). Both ways rely on the gompy plugin, so the first thing to do
is to compile it (for now you need to do it, in the future there will be precompiled wheels)
You need to install Python3.
- Under Linux, you can use the standard distribution package. You will need to install also
the development package (
python3-xxx-dev) - Under Windows, I recommend the Anaconda distribution
- Edit
GraphiteThree/plugins/OGF/plugins.txt, add the following line:
add_subdirectory(gompy)
- Re-build Graphite. You will need to re-configure (
configure.shorconfigure.bat) then build withCMake(follow the instructions here)
- start Graphite, open the
Programsmodule (left toolbar, see Figure) - in the
Filemenu of theProgramsmodule, selectNew->Python. If the entry is not there in the menu, it means thatgompywas not properly compiled or installed - in the editor, type
print("hello from Python")then run the program by pressing<F5>
Let us now create a more interesting program. First thing, we will create two spheres, as follows:
# Python
scene_graph.clear()
S1 = scene_graph.create_mesh('S1')
S1.I.Shapes.create_sphere(center=[0,0,0])
S2 = scene_graph.create_mesh('S2')
S2.I.Shapes.create_sphere(center=[0.5,0,0])Everything that you can do in the Graphite interface, you can script it in Python. The scene_graph is the main Graphite object, that contains all the shapes that you will create. In the first line, we clear it (then when running the script multiple times, you will restart from a fresh scenegraph). Then we create a mesh. Objects are created in the scenegraph using the create_mesh function, that takes the name of the mesh to create as an argument, as it will appear in the left toolbar of Graphite. There also exists a create_object function that takes the classname of the object (if set to OGF::MeshGrob, it does the same thing as create_mesh, and there are other Graphite object classes that you can use, for voxel objects for instance).
Then we create a sphere. If you were doing that manually, you would use the menu Surface->Shapes->create sphere. Programatically, the menus correspond to Interfaces. A Graphite object can have multiple Interfaces, they are accessed through object.I.xxx where xxx is the interface name. Note that Graphite's programming editor has automatic completion, it helps a lot ! By hovering a word in the editor, you also obtain some documentation in a help bubble.
OK, so we do that a second time to create another sphere, shifted to the right. If you press <F5> now, you will see both spheres appearing.
Now we can compute the difference between both spheres and hide the initial spheres (to better see the result), as follows (press '' again to see the result):
S1.I.Surface.compute_difference(other=S2,result='difference')
S1.visible=False
S2.visible=False
Let us see now how Graphite commands can be imported in an existing Python environment. Graphite has a built-in tool to do that, it is available from the Programs module, Examples->Python menu, install_gompy.lua entry, as shown in the Figure above. Run the script with <F5>, this will install gompy in the first writeable Python environment declared in PYTHON_PATH (If you want to install gompy in a specific Python environment, make sure it appears first in PYTHON_PATH before starting Graphite). This generates a small Python initialization code, that loads
Graphite DLLs/shared objects into the Python interpreter and connects the functions to it (Do not delete Graphite after that, only a tiny Python script with references to Graphite library is generated in the Python environment, the DLLs/shared objects are not copied).
Now you can use all Graphite commands in Python ! Start your Python interpreter and import Graphite's module (gompy). If everything goes well, you should see something like:
$ python3
Python 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import gompy
o-[ModuleMgr ] Loading module: luagrob
o-[ModuleMgr ] Loading module: mesh
o-[ModuleMgr ] Loading module: voxel
>>>
Now you can write some Python scripts. Here is a small example program that computes the difference between two spheres and saves it to a file:
import gompy
scene_graph = gom.meta_types.OGF.SceneGraph.create()
S1 = scene_graph.create_object(classname='OGF::MeshGrob',name='S1')
S2 = scene_graph.create_object(classname='OGF::MeshGrob',name='S2')
S1.I.Shapes.create_sphere(center=[0,0,0])
S2.I.Shapes.create_sphere(center=[0,0,0.5])
S1.I.Surface.compute_difference(other=S2,result='R')
scene_graph.objects.R.save('difference.obj')There is a small difference as compared to scripts written in Python in Graphite mode: when you start, no Graphite object exists, so you need to create the scenegraph. It is created using the Graphite object model, projected into Python, accessed through gom.meta_types. Once the scenegraph is created, you can manipulate it just as we previously did in Graphite.
You may find it not super convenient to create objects in the Python script and visualize them in an external program. Fortunately there is Polyscope, an easy-to-use library to visualize polygon meshes (and much more), and it has Python bindings that take numpy arrays. It can be installed through pip:
$ pip install polyscope
Let us see how to make it display a Graphite mesh:
import polyscope as ps
import numpy as np
import gompy # import it *after* polyscope, else it makes polyscope crash
def register_graphite_object(O):
pts = np.asarray(O.I.Editor.find_attribute('vertices.point'))
tri = np.asarray(O.I.Editor.get_triangles())
ps.register_surface_mesh(O.name,pts,tri)
def register_graphite_objects():
for i in dir(scene_graph.objects):
register_graphite_object(scene_graph.resolve(i))
scene_graph = gom.meta_types.OGF.SceneGraph.create()
S1 = scene_graph.create_object('Mesh','S1')
S1.I.Shapes.create_sphere(center=[0,0,0])
S2 = scene_graph.create_object('Mesh','S2')
S2.I.Shapes.create_sphere(center=[0.5,0,0])
S1.I.Surface.compute_intersection(S2,'S')
ps.init()
register_graphite_objects()
ps.show()The function register_graphite_objects() sends the whole Graphite scenegraph to polyscope, that displays it when entering its event loop with ps.show(). Graphite and polyscope were developed independently, but since they both have a NumPy API, they can talk together, and this happens without copying any data.
We shall now see how to compute the vibration modes of a violin and display them using pyPlotLib.
The Python script is available in Graphite's Python programming examples (use the Programs module, and load it from the Examples->Python menu). You can also get the raw file from the repository here.
Let us see how this file works, chunk by chunk. First thing, we'll need to import a couple of modules:
import sys,math,numpy,os.pathIt is easy to write scripts that work in both Python in Graphite and Graphite in Python modes, just start your script as follows:
if not 'gom' in globals():
import gompy
scene_graph = gom.meta_types.OGF.SceneGraph.create()
else:
# pyplot accesses sys.argv[0] that is not initialized by Graphite
sys.argv = ['graphite']If we are in Graphite in Python mode, then gom does not exists, so we import gompy and create the scenegraph. Else there is a tiny thing to do to make pyplotlib happy.
Then we load the .obj file with the violin's geometry (or create an octogon if the file was not present). The PROJECT_ROOT gom environement variable points to the Graphite installation (note: it is not a true environment variable, it is internal to Graphite).
file = gom.get_environment_value('PROJECT_ROOT')+'/lib/data/violin.obj'
if os.path.isfile(file):
S = scene_graph.load_object(file)
else:
S = scene_graph.create_object('Mesh','S').I.Shapes.create_ngon(nb_edges=8)Then we remesh the object, and compute the manifold harmonics:
S.I.Surface.remesh_smooth(nb_points=500,remesh_name='remesh')
R = scene_graph.objects.remesh
R.I.Spectral.compute_manifold_harmonics(nb_eigens=100)The command remesh_smooth() creates by default a surface named remesh (can be changed with its arguments). It is then accessed through scene_graph.objects.remesh.
Now we are going to display the result using matplotlib. So we need to import a couple of packages:
import matplotlib.pyplot as plt
import matplotlib.tri as mtri
import matplotlib.cm as cmMatplotlib uses numpy arrays. There is a way of seeing Graphite objects, their point coordinates and their attributes as numpy arrays, as follows:
XYZ = numpy.asarray(R.I.Editor.find_attribute('vertices.point'))
VV = numpy.asarray(R.I.Editor.find_attribute('vertices.eigen'))
T = numpy.asarray(R.I.Editor.get_triangles())
X = XYZ[:,0]
Y = XYZ[:,1]This reads the points coordinates (XYZ), the manifold harmonics (VV), the mesh triangle indices (T) using the Editor interface of the MeshGrob class. The Editor interface provides a low-level access to the mesh, its geometry and attributes. Interestingly, no memory is copied. It can be also used to modify the coordinates of the mesh vertices.
Finally, the X and Y components of the points coordinates are extracted in separate arrays.
Now that everything is accessible through standard numpy arrays, we can display nice contours using pyplotlib, as follows:
triang = mtri.Triangulation(X,Y,T)
def plot_eigen(n):
plt.gca().set_aspect('equal')
plt.tricontourf(triang, VV[:,n])
plt.triplot(triang,'k-')
plt.title('eigen' + str(n))
def highres_contours_plot_eigen(n):
plt.gca().set_aspect('equal')
z = VV[:,n]
refiner = mtri.UniformTriRefiner(triang)
tri_refi, z_test_refi = refiner.refine_field(z, subdiv=3)
zmin = numpy.amin(z)
zmax = numpy.amax(z)
levels = numpy.arange(zmin, zmax, 0.03*(zmax-zmin))
cmap = cm.get_cmap(name='terrain', lut=None)
plt.tricontourf(tri_refi, z_test_refi, levels=levels, cmap=cmap)
plt.tricontour(tri_refi, z_test_refi, levels=levels,
colors=['0.25', '0.5', '0.5', '0.5', '0.5'],
linewidths=[1.0, 0.5, 0.5, 0.5, 0.5])
plt.title('eigen' + str(n))
plt.figure()
for n in range(1,5):
plt.subplot(220+n)
highres_contours_plot_eigen(n*10)
plt.show()Using gompy in Jupyter notebooks works just the same. Start jupyter notebook from the Python environment where you installed gompy:
$ jupyter-notebook
We shall see now how to do the same example in Jupyter. The notebook is here: MH2D.ipynb. Let us create it step by step:
First, create a new notebook called MH2d. Then, create a cell with:
%matplotlib inline
import gompy
scene_graph = gom.meta_types.OGF.SceneGraph.create()Run the cell, create a new cell with:
file = gom.get_environment_value('PROJECT_ROOT')+'/lib/data/violin.obj'
S = scene_graph.load_object(file)This will load the mesh from the violin.obj file shipped with Graphite. Now we can remesh it and compute the Manifold Harmonics:
S.I.Surface.remesh_smooth(nb_points=1000,remesh_name='remesh')
R = scene_graph.objects.remesh
R.I.Spectral.compute_manifold_harmonics(nb_eigens=100)Then, we access the mesh and computed values as NumPy arrays:
import numpy
XYZ = numpy.asarray(R.I.Editor.find_attribute('vertices.point'))
VV = numpy.asarray(R.I.Editor.find_attribute('vertices.eigen'))
T = numpy.asarray(R.I.Editor.get_triangles())
X = XYZ[:,0]
Y = XYZ[:,1]A good thing with Jupyter notebooks is that we can easily generate intermediate visualizations at any step. Let us take a look at our mesh:
import matplotlib.pyplot as plt
import matplotlib.tri as mtri
import matplotlib.cm as cm
triang = mtri.Triangulation(X,Y,T)
plt.figure(figsize=(16,8))
plt.triplot(triang)
plt.show()
Now we can take a look at the Manifold Harmonics. For that we define a new function:
def plot_eigen(n):
plt.gca().set_aspect('equal')
plt.tricontourf(triang, VV[:,n])
plt.triplot(triang,'k-')
plt.title('eigen' + str(n))And use it as follows:
plt.figure(figsize=(16,8))
for n in range(1,5):
plt.subplot(220+n)
plot_eigen(n*10)
plt.show()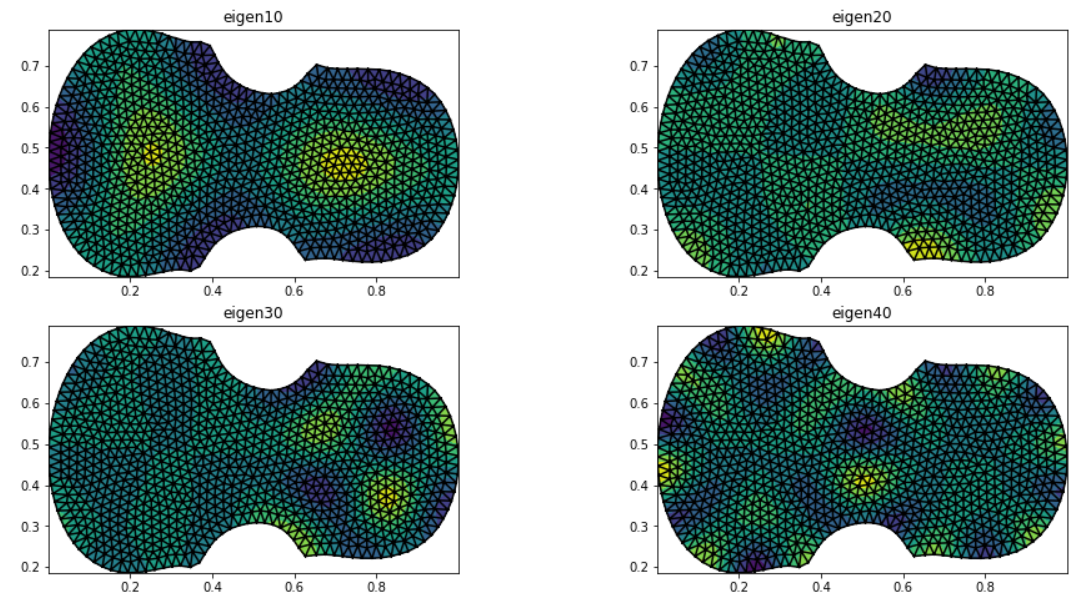
To better see the variations of the Manifold Harmonics, one can use isocontour lines, as follows:
def highres_contours_plot_eigen(n):
plt.gca().set_aspect('equal')
z = VV[:,n]
refiner = mtri.UniformTriRefiner(triang)
tri_refi, z_test_refi = refiner.refine_field(z, subdiv=3)
zmin = numpy.amin(z)
zmax = numpy.amax(z)
levels = numpy.arange(zmin, zmax, 0.04*(zmax-zmin))
cmap = cm.get_cmap(name='terrain', lut=None)
plt.tricontourf(tri_refi, z_test_refi, levels=levels, cmap=cmap)
x = plt.tricontour(tri_refi, z_test_refi, levels=levels,
colors=['0.25', '0.5', '0.5', '0.5', '0.5'],
linewidths=[1.0, 0.5, 0.5, 0.5, 0.5])
plt.title('eigen' + str(n))
plt.figure(figsize=(9,9))
highres_contours_plot_eigen(58)
plt.show()
... you can also display several ones on the same figure:
plt.figure(figsize=(9,9))
for n in range(1,5):
plt.subplot(220+n)
highres_contours_plot_eigen(n*10)
plt.show()
- use autocompletion (
<tab>key), works in Graphite, in Python interpreter and in Jupyter - use the documentation: in Jupyter Notebook, push
<shift>then<tab>twice right after an object or function name. You can also print the__doc__attribute, for instance:
S = scene_graph.load_object(filename)
print(S.I.Spectral.compute_manifold_harmonics.__doc__)and this will say:
GOM function
============
OGF::MeshGrobSpectralCommands::compute_manifold_harmonics(nb_eigens,discretization,attribute,shift,nb_eigens_per_band,print_spectrum)
Computes manifold harmonics (Laplacien eigenfunctions)
Parameters
==========
nb_eigens : unsigned int = 30
number of eigenfunctions to compute
discretization : GEO::LaplaceBeltramiDiscretization = FEM_P1_LUMPED
discretization of the Laplace Beltrami operator
attribute : std::string = 'eigen'
name of the attribute used to store the eigenvectors
shift : double = 0
eigen shift applied to explore a certain part of the spectrum.
nb_eigens_per_band : unsigned int = 0
if non-zero, use band-by-band computation.
print_spectrum : bool = false
if true, prints eigenvalue to the terminal.
- The list of all commands that one can apply to a mesh is here. Note that the interface to use may differ from the menu name.