-
Notifications
You must be signed in to change notification settings - Fork 1.1k
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Merge branch 'main' of https://github.com/itcharge/LeetCode-Py
- Loading branch information
Showing
8 changed files
with
520 additions
and
2 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,106 @@ | ||
| # [1041. 困于环中的机器人](https://leetcode.cn/problems/robot-bounded-in-circle/) | ||
|
|
||
| - 标签:数学、字符串、模拟 | ||
| - 难度:中等 | ||
|
|
||
| ## 题目链接 | ||
|
|
||
| - [1041. 困于环中的机器人 - 力扣](https://leetcode.cn/problems/robot-bounded-in-circle/) | ||
|
|
||
| ## 题目大意 | ||
|
|
||
| **描述**:在无限的平面上,机器人最初位于 $(0, 0)$ 处,面朝北方。注意: | ||
|
|
||
| - 北方向 是 $y$ 轴的正方向。 | ||
| - 南方向 是 $y$ 轴的负方向。 | ||
| - 东方向 是 $x$ 轴的正方向。 | ||
| - 西方向 是 $x$ 轴的负方向。 | ||
|
|
||
| 机器人可以接受下列三条指令之一: | ||
|
|
||
| - `"G"`:直走 $1$ 个单位 | ||
| - `"L"`:左转 $90$ 度 | ||
| - `"R"`:右转 $90$ 度 | ||
|
|
||
| 给定一个字符串 $instructions$,机器人按顺序执行指令 $instructions$,并一直重复它们。 | ||
|
|
||
| **要求**:只有在平面中存在环使得机器人永远无法离开时,返回 $True$。否则,返回 $False$。 | ||
|
|
||
| **说明**: | ||
|
|
||
| - $1 \le instructions.length \le 100$。 | ||
| - $instructions[i]$ 仅包含 `'G'`,`'L'`,`'R'`。 | ||
|
|
||
| **示例**: | ||
|
|
||
| - 示例 1: | ||
|
|
||
| ```python | ||
| 输入:instructions = "GGLLGG" | ||
| 输出:True | ||
| 解释:机器人最初在(0,0)处,面向北方。 | ||
| “G”:移动一步。位置:(0,1)方向:北。 | ||
| “G”:移动一步。位置:(0,2).方向:北。 | ||
| “L”:逆时针旋转90度。位置:(0,2).方向:西。 | ||
| “L”:逆时针旋转90度。位置:(0,2)方向:南。 | ||
| “G”:移动一步。位置:(0,1)方向:南。 | ||
| “G”:移动一步。位置:(0,0)方向:南。 | ||
| 重复指令,机器人进入循环:(0,0)——>(0,1)——>(0,2)——>(0,1)——>(0,0)。 | ||
| 在此基础上,我们返回 True。 | ||
| ``` | ||
|
|
||
| - 示例 2: | ||
|
|
||
| ```python | ||
| 输入:instructions = "GG" | ||
| 输出:False | ||
| 解释:机器人最初在(0,0)处,面向北方。 | ||
| “G”:移动一步。位置:(0,1)方向:北。 | ||
| “G”:移动一步。位置:(0,2).方向:北。 | ||
| 重复这些指示,继续朝北前进,不会进入循环。 | ||
| 在此基础上,返回 False。 | ||
| ``` | ||
|
|
||
| ## 解题思路 | ||
|
|
||
| ### 思路 1:模拟 | ||
|
|
||
| 设定初始位置为 $(0, 0)$,初始方向 $direction = 0$,假设按照给定字符串 $instructions$ 执行一遍之后,位于 $(x, y)$ 处,且方向为 $direction$,则可能出现的所有情况为: | ||
|
|
||
| 1. 方向不变($direction == 0$),且 $(x, y) == (0, 0)$,则会一直在原点,无法走出去。 | ||
| 2. 方向不变($direction == 0$),且 $(x, y) \ne (0, 0)$,则可以走出去。 | ||
| 3. 方向相反($direction == 2$),无论是否产生位移,则再执行 $1$ 遍将会回到原点。 | ||
| 4. 方向逆时针 / 顺时针改变 $90°$($direction == 1 \text{ or } 3$),无论是否产生位移,则再执行 $3$ 遍将会回到原点。 | ||
|
|
||
| 综上所述,最多模拟 $4$ 次即可知道能否回到原点。 | ||
|
|
||
| 从上面也可以等出结论:如果不产生位移,则一定会回到原点。如果改变方向,同样一定会回到原点。 | ||
|
|
||
| 我们只需要根据以上结论,按照 $instructions$ 执行一遍之后,通过判断是否产生位移和改变方向,即可判断是否一定会回到原点。 | ||
|
|
||
| ### 思路 1:代码 | ||
|
|
||
| ```Python | ||
| class Solution: | ||
| def isRobotBounded(self, instructions: str) -> bool: | ||
| # 分别代表北、东、南、西 | ||
| directions = [(0, 1), (-1, 0), (0, -1), (1, 0)] | ||
| x, y = 0, 0 | ||
| # 初始方向为北 | ||
| direction = 0 | ||
| for step in instructions: | ||
| if step == 'G': | ||
| x += directions[direction][0] | ||
| y += directions[direction][1] | ||
| elif step == 'L': | ||
| direction = (direction + 1) % 4 | ||
| else: | ||
| direction = (direction + 3) % 4 | ||
|
|
||
| return (x == 0 and y == 0) or direction != 0 | ||
| ``` | ||
|
|
||
| ### 思路 1:复杂度分析 | ||
|
|
||
| - **时间复杂度**:$O(n)$,其中 $n$ 为字符串 $instructions$ 的长度。 | ||
| - **空间复杂度**:$O(1)$。 |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,98 @@ | ||
| # [1110. 删点成林](https://leetcode.cn/problems/delete-nodes-and-return-forest/) | ||
|
|
||
| - 标签:树、深度优先搜索、数组、哈希表、二叉树 | ||
| - 难度:中等 | ||
|
|
||
| ## 题目链接 | ||
|
|
||
| - [1110. 删点成林 - 力扣](https://leetcode.cn/problems/delete-nodes-and-return-forest/) | ||
|
|
||
| ## 题目大意 | ||
|
|
||
| **描述**:给定二叉树的根节点 $root$,树上每个节点都有一个不同的值。 | ||
|
|
||
| 如果节点值在 $to\underline{}delete$ 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。 | ||
|
|
||
| **要求**:返回森林中的每棵树。你可以按任意顺序组织答案。 | ||
|
|
||
| **说明**: | ||
|
|
||
| - 树中的节点数最大为 $1000$。 | ||
| - 每个节点都有一个介于 $1$ 到 $1000$ 之间的值,且各不相同。 | ||
| - $to\underline{}delete.length \le 1000$。 | ||
| - $to\underline{}delete$ 包含一些从 $1$ 到 $1000$、各不相同的值。 | ||
|
|
||
| **示例**: | ||
|
|
||
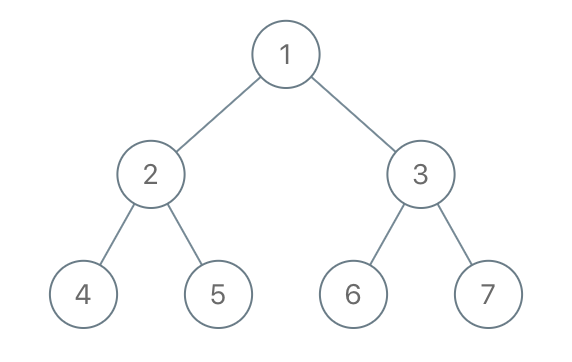
| - 示例 1: | ||
|
|
||
|  | ||
|
|
||
| ```python | ||
| 输入:root = [1,2,3,4,5,6,7], to_delete = [3,5] | ||
| 输出:[[1,2,null,4],[6],[7]] | ||
| ``` | ||
|
|
||
| - 示例 2: | ||
|
|
||
| ```python | ||
| 输入:root = [1,2,4,null,3], to_delete = [3] | ||
| 输出:[[1,2,4]] | ||
| ``` | ||
|
|
||
| ## 解题思路 | ||
|
|
||
| ### 思路 1:深度优先搜索 | ||
|
|
||
| 将待删除节点数组 $to\underline{}delete$ 转为集合 $deletes$,则每次能以 $O(1)$ 的时间复杂度判断节点值是否在待删除节点数组中。 | ||
|
|
||
| 如果当前节点值在待删除节点数组中,则删除当前节点后,我们还需要判断其左右子节点是否也在待删除节点数组中。 | ||
|
|
||
| 以此类推,还需要判断左右子节点的左右子节点。。。 | ||
|
|
||
| 因此,我们应该递归遍历处理完所有的左右子树,再判断当前节点的左右子节点是否在待删除节点数组中。如果在,则将其加入到答案数组中。 | ||
|
|
||
| 为此我们可以写一个深度优先搜索算法,具体步骤如下: | ||
|
|
||
| 1. 如果当前根节点为空,则返回 `None`。 | ||
| 2. 递归遍历处理完当前根节点的左右子树,更新当前节点的左右子树(子节点被删除的情况下需要更新当前根节点的左右子树)。 | ||
| 3. 如果当前根节点值在待删除节点数组中: | ||
| 1. 如果当前根节点的左子树没有在被删除节点数组中,将左子树节点加入到答案数组中。 | ||
| 2. 如果当前根节点的右子树没有在被删除节点数组中,将右子树节点加入到答案数组中。 | ||
| 3. 返回 `None`,表示当前节点被删除。 | ||
| 4. 如果当前根节点值不在待删除节点数组中: | ||
| 1. 返回根节点,表示当前节点没有被删除。 | ||
|
|
||
| ### 思路 1:代码 | ||
|
|
||
| ```Python | ||
| class Solution: | ||
| def delNodes(self, root: Optional[TreeNode], to_delete: List[int]) -> List[TreeNode]: | ||
| forest = [] | ||
| deletes = set(to_delete) | ||
| def dfs(root): | ||
| if not root: | ||
| return None | ||
| root.left = dfs(root.left) | ||
| root.right = dfs(root.right) | ||
|
|
||
| if root.val in deletes: | ||
| if root.left: | ||
| forest.append(root.left) | ||
| if root.right: | ||
| forest.append(root.right) | ||
| return None | ||
| else: | ||
| return root | ||
|
|
||
|
|
||
| if dfs(root): | ||
| forest.append(root) | ||
| return forest | ||
| ``` | ||
|
|
||
| ### 思路 1:复杂度分析 | ||
|
|
||
| - **时间复杂度**:$O(n)$,其中 $n$ 为二叉树中节点个数。 | ||
| - **空间复杂度**:$O(n)$。 | ||
|
|
Oops, something went wrong.