-
Notifications
You must be signed in to change notification settings - Fork 32
1D 123 Test
This test highlights a scenario in which linearized Riemann solvers will produce negative densities/pressures without appropriate modifications. This is due to a region of mostly kinetic energy and approaching vacuum pressure. However, cholla checks densities/pressure produced by the approximate (Roe) solver and switches to the HLLE solver if needed. This is not an issue with the exact solver. This test is from Toro's Riemann solvers and numerical methods for fluid dynamics Sec. 6.3.3, test 2. The test consists of left and right states separated at x = 0.5 with velocities -2 and 2, respectively, moving away from each other. Density = 1.0 and pressure = 0.4 on both sides. Gamma is set to 1.4. This test is performed with the hydro build (cholla/builds/make.type.hydro) and Van Leer integrator. Full initial conditions can be found in cholla/src/grid/initial_conditions.cppunder Riemann().
#
# Parameter File for Einfeldt strong rarefaction test (aka 123 problem)
# Parameters derived from Toro, Sec. 6.4.4, test 2
#
################################################
# number of grid cells in the x dimension
nx=128
# number of grid cells in the y dimension
ny=1
# number of grid cells in the z dimension
nz=1
# final output time
tout=0.15
# time interval for output
outstep=0.15
# name of initial conditions
init=Riemann
# domain properties
xmin=0.0
ymin=0.0
zmin=0.0
xlen=1.0
ylen=1.0
zlen=1.0
# type of boundary conditions
xl_bcnd=3
xu_bcnd=3
yl_bcnd=0
yu_bcnd=0
zl_bcnd=0
zu_bcnd=0
# path to output directory
outdir=./
#################################################
# Parameters for 1D Riemann problems
# density of left state
rho_l=1.0
# velocity of left state
vx_l=-2.0
vy_l=0.0
vz_l=0.0
# pressure of left state
P_l=0.4
# density of right state
rho_r=1.0
# velocity of right state
vx_r=2.0
vy_r=0.0
vz_r=0.0
# pressure of right state
P_r=0.4
# location of initial discontinuity
diaph=0.5
# value of gamma
gamma=1.4
Upon completion, you should obtain 2 output files. The initial and final density, pressure, and velocity (in code units) of the solution is shown below (pink dots) plotted over the exact solution (purple line). Examples of how to extract and plot data can be found in cholla/python_scripts/plot_sod.ipynb.
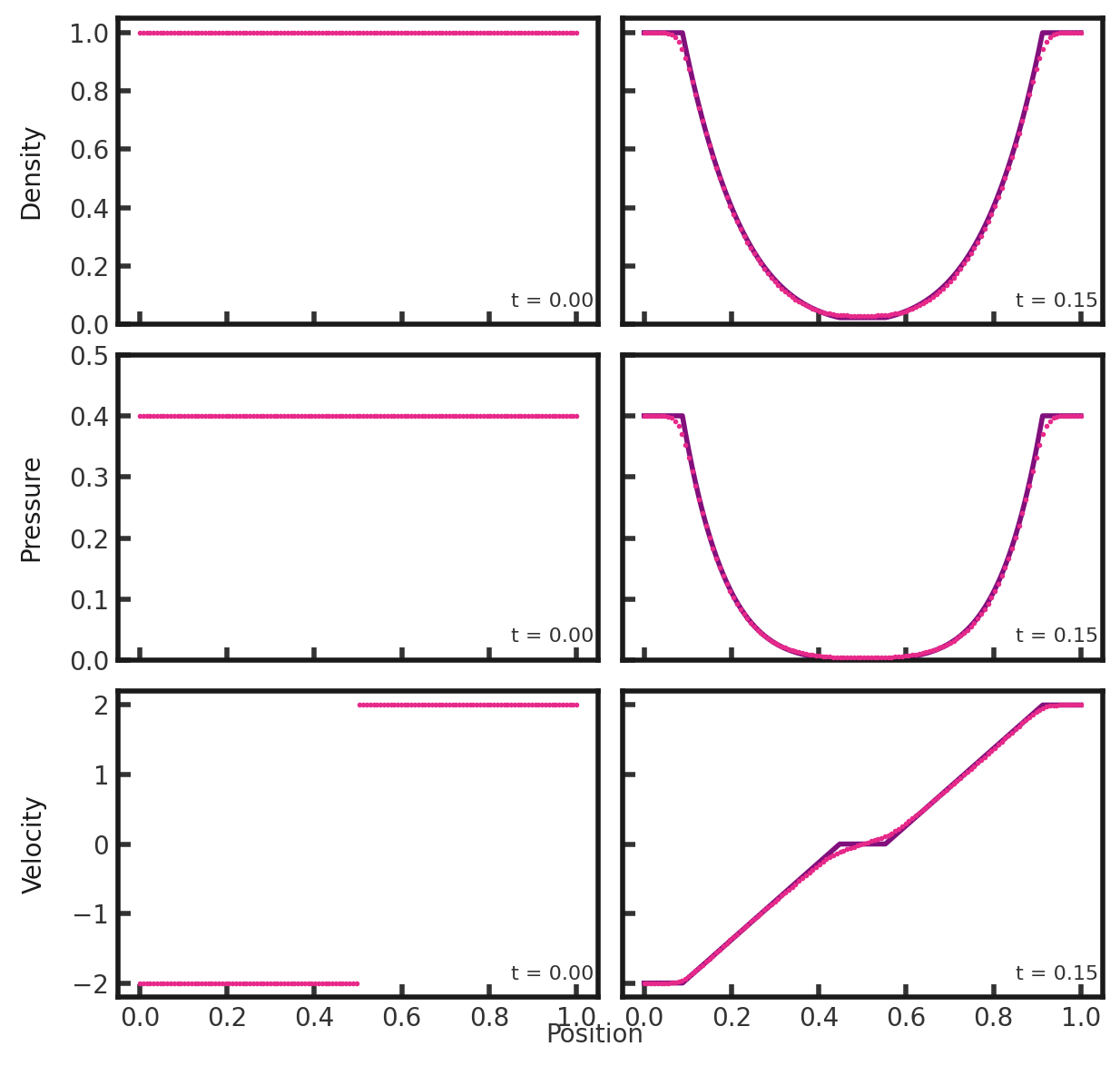
We see that the two rarefaction waves have moved outwards, away from each other, leaving behind a region of low density and low pressure.