Skip to content

1D Sod

Jump to bottom Edit New page
evazlimen edited this page Jul 16, 2024 · 2 revisions

1D Sod Shock Tube

This test highlights the ability of a code to resolve shocks and contact discontinuities over a narrow region. Parameters from Sod (1978). The setup consists of a density and pressure of 1.0 for x < 0 and 0.1 for x > 0.5. Gamma is set to 1.4. This test was performed with the hydro build (cholla/builds/make.type.hydro) and Van Leer integrator. Full initial conditions can be found in cholla/src/grid/initial_conditions.cppunder Riemann().

Parameter file: (cholla/examples/1D/sod.txt)

#
# Parameter File for 1D Sod Shock tube
#

################################################
# number of grid cells in the x dimension
nx=100
# number of grid cells in the y dimension
ny=1
# number of grid cells in the z dimension
nz=1
# final output time
tout=0.2
# time interval for output
outstep=0.2
# name of initial conditions
init=Riemann
# domain properties
xmin=0.0
ymin=0.0
zmin=0.0
xlen=1.0
ylen=1.0
zlen=1.0
# type of boundary conditions
xl_bcnd=3
xu_bcnd=3
yl_bcnd=0
yu_bcnd=0
zl_bcnd=0
zu_bcnd=0
# path to output directory
outdir=./

#################################################
# Parameters for 1D Riemann problems
# density of left state
rho_l=1.0
# velocity of left state
vx_l=0.0
vy_l=0.0
vz_l=0.0
# pressure of left state
P_l=1.0
# density of right state
rho_r=0.1
# velocity of right state
vx_r=0.0
vy_r=0.0
vz_r=0.0
# pressure of right state
P_r=0.1
# location of initial discontinuity
diaph=0.5
# value of gamma
gamma=1.4

Upon completion, you should obtain two output files.The initial and final density, pressure, and velocity (in code units) of the solution is shown below (pink dots) plotted over the exact solution (purple line). Examples of how to extract and plot data can be found in cholla/python_scripts/plot_sod.ipynb.
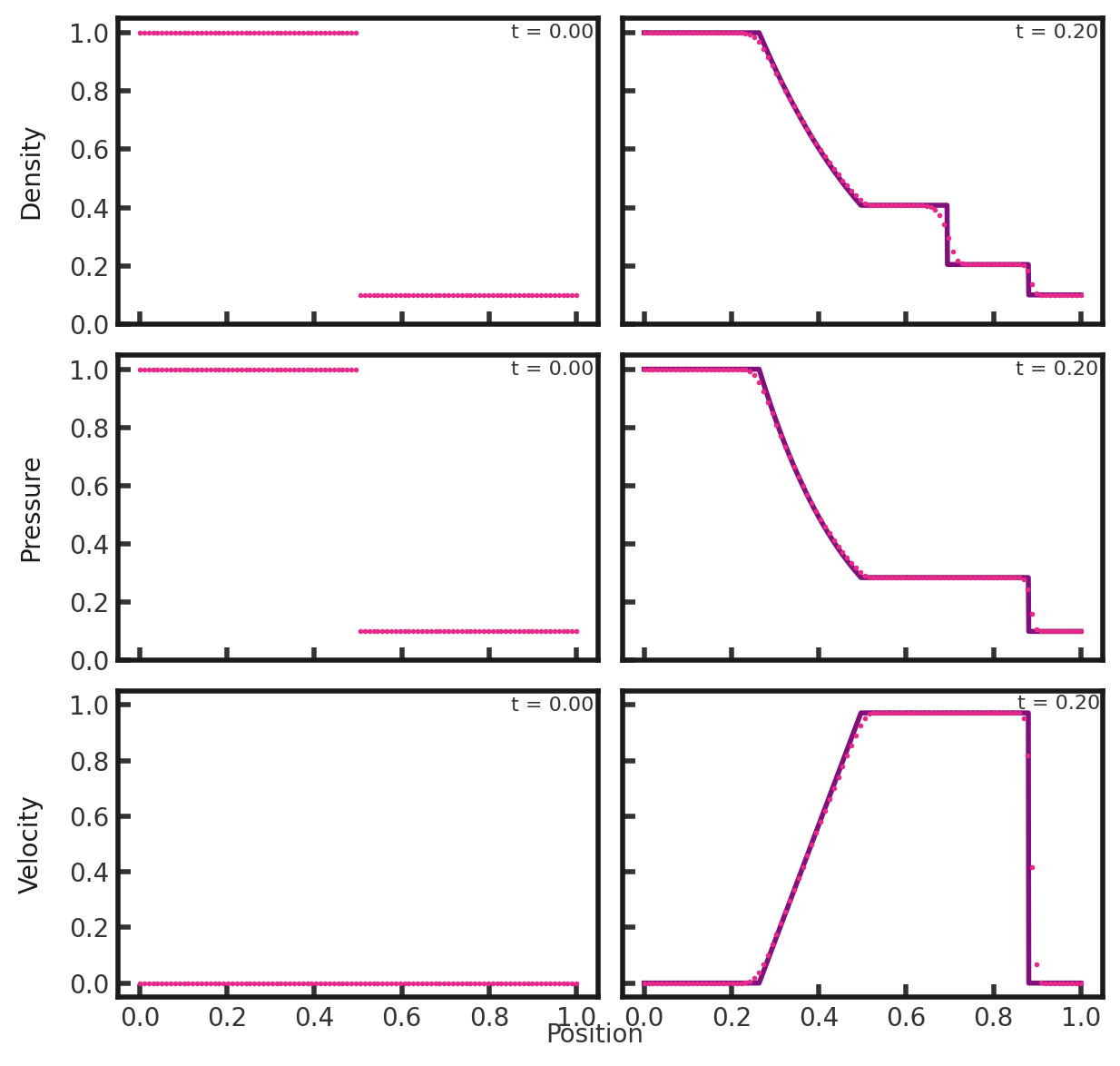
Three rows of two scatter plots side by side. The first row shows density vs x position while the second shows pressure vs x position and the third shows velocity vs x position. In all rows, the first plot has the text 't = 0.00' in the upper right corner while the second plot has the text 't = 0.20' in the upper right corner. The plots of the first column are shown with pink dots while the plots of the second column have pink dots plotted over a purple line. In all cases, the pink dots match the shape of the purple line, albeit imperfectly. The first plot in the first row (initial density) shows a density of 1.0 for x = 0 to x= 0.5 and a density of 0.1 for the remaining x values. The second (final density) plot shows a density of 1.0 for 0 \< x \< 0.2, then a continuous gradual decrease to a value of 0.4 at x = 0.5. Density remains constant until x = 0.7, then it jumps down abruptly to a value of 0.2. Density remains constant here until x = 0.9 where it makes a final jump to a value of 0.1, remaining at 0.1 for the final x values. In the second row, the first plot (initial pressure) is identical to the initial density plot. The second plot (final pressure) shows a pressure of 1.0 for 0 \< x \< 0.2, then a continuous gradual decrease to a value of 0.3 at x = 0.5. Pressure remains constant until x = 0.9 where it makes a jump to a value of 0.1, remaining at 0.1 for the final x values. In the third row, the first plot (initial velocity) shows a constant value of zero across the grid. The second plot (final velocity) shows a value of 0 until just after x = 0.2 where it begins to increase to a value of 0.8 by x = 0.5. It remains constant until x = 0.9 where it drops back to zero.

We see a rarefaction wave propagating away from the initial discontinuity, a contact discontinuity at x = 0.7, and a shock at x =0.9. cholla's solution is in agreement with the exact solution, however we notice that the contact discontinuty and shock are marginaly less narrowly resolved than in the exact solution.

Add a custom footer

Cholla Wiki

Physics

Testing

Examples

Advanced

In progress

Contributing

Clone this wiki locally